前言

这几天在学习Joern源码，在看到CFG生成原理的时候还是挺顺利的，但是学到生成DDG，也就是Data-Flow-Graph的时候，就一脸懵。跟踪调试了几遍都没有搞懂，后来google了如何通过CFG生成DDG发现了一些文章：

https://www.cnblogs.com/kexinxin/p/10147196.html

https://chengxiao19961022.github.io/2019/03/04/%E9%9D%99%E6%80%81%E6%95%B0%E6%8D%AE%E6%B5%81%E5%88%86%E6%9E%90/

https://liuyehcf.github.io/2017/11/23/%E7%BC%96%E8%AF%91%E5%8E%9F%E7%90%86-%E4%BB%A3%E7%A0%81%E4%BC%98%E5%8C%962/

我这才意识到这和编译原理的代码优化有关。突然想起南京大学Yue Li老师和Tian Tan老师之前开设的静态程序分析课程。去年暑假的时候偶然有看到过，但是没有具体的学习目标就没继续学习，这次重新捡起来看，发现刚好解决了我的困惑，只是可惜课程的视频讲解只有8节（本来应该有16节），在bilibili可以观看：https://space.bilibili.com/2919428?spm_id_from=333.788.b_765f7570696e666f.1

老师的课件也做得非常详尽美观，是很好的学习资料。

数据流分析简介

什么是数据流分析？数据流分析是一项编译时使用的技术，它能从程序代码中收集程序的语义信息，并通过代数的方法在编译时确定变量的定义和使用。通过数据流分析，可以不必实际运行程序就能够发现程序运行时的一些行为，可以帮助大家更好地理解程序。数据流分析被用于解决编译优化、程序验证、调试、测试、并行、向量化和并行编程环境等问题。简单地说，数据流分析就是，对程序中数据的使用、定义及其之间的依赖关系等各方面信息进行收集的过程。

数据流分析有多种解决方法：

  1. 强连通区域方法；
  2. 迭代算法；
  3. T1-T2分析；
  4. 结点列表算法；
  5. 图形文法方法；
  6. 消去法，比如，区间分析；
  7. 高级语法制导的方法；
  8. 结构分析；
  9. 为止式（slotwise）分析。

以上关于数据流的定义内容参考自：

[1]汪小飞, 赵克佳, 田祖伟. 数据流分析的关键技术研究[J]. 计算机科学, 2005, 032(012):91-93.

其中本节课老师教授的内容就是迭代算法，它也是最常用也是最实用的一种方法。

over-approximation

静态分析应该从下面两个方向来进行把握：

  1. 对data做abstraction，这个abstraction有很多种形式，看我们需要什么，比如：

    5

    其中T表示undefined，倒T表示unknown。

  2. 对flow做over-approximation

什么是over-approximation？程序在动态运行时，无论在什么输入下，走任何的执行路径，所能产生的值，静态分析都应该能够预测到，称其为over-approximation，也就是对程序的行为做一个模拟，来得到近似程序执行时的行为。

举个例子，变量x在执行时遇到了两条分支，一条是-x操作，另一个条是+x操作，求x在下一个汇聚点时值是正还是负？对于这种要求，我们只能将-x和+x都考虑进来，因为都存在可能性，这就叫做over-approximation。

1

对于绝大多数的静态分析来说都是进行的over-approximation，对于这类静态分析，称其为may analysis。

另一类静态分析要求输出的信息都必须是准确的，也就是under-approximation，对于这类静态分析，称其为must analysis。

但是无论是must analysis还是may analysis，都是为了程序分析的安全性。

2

综合起来，我们纠正一下开头的说法，静态分析应该从下面两个方向来进行把握：

  1. 对data做abstraction
  2. 对flow做safe-approximation

对于may analysis来说，safe的涵义是over；对于must analysis来说，safe的涵义是under。

3

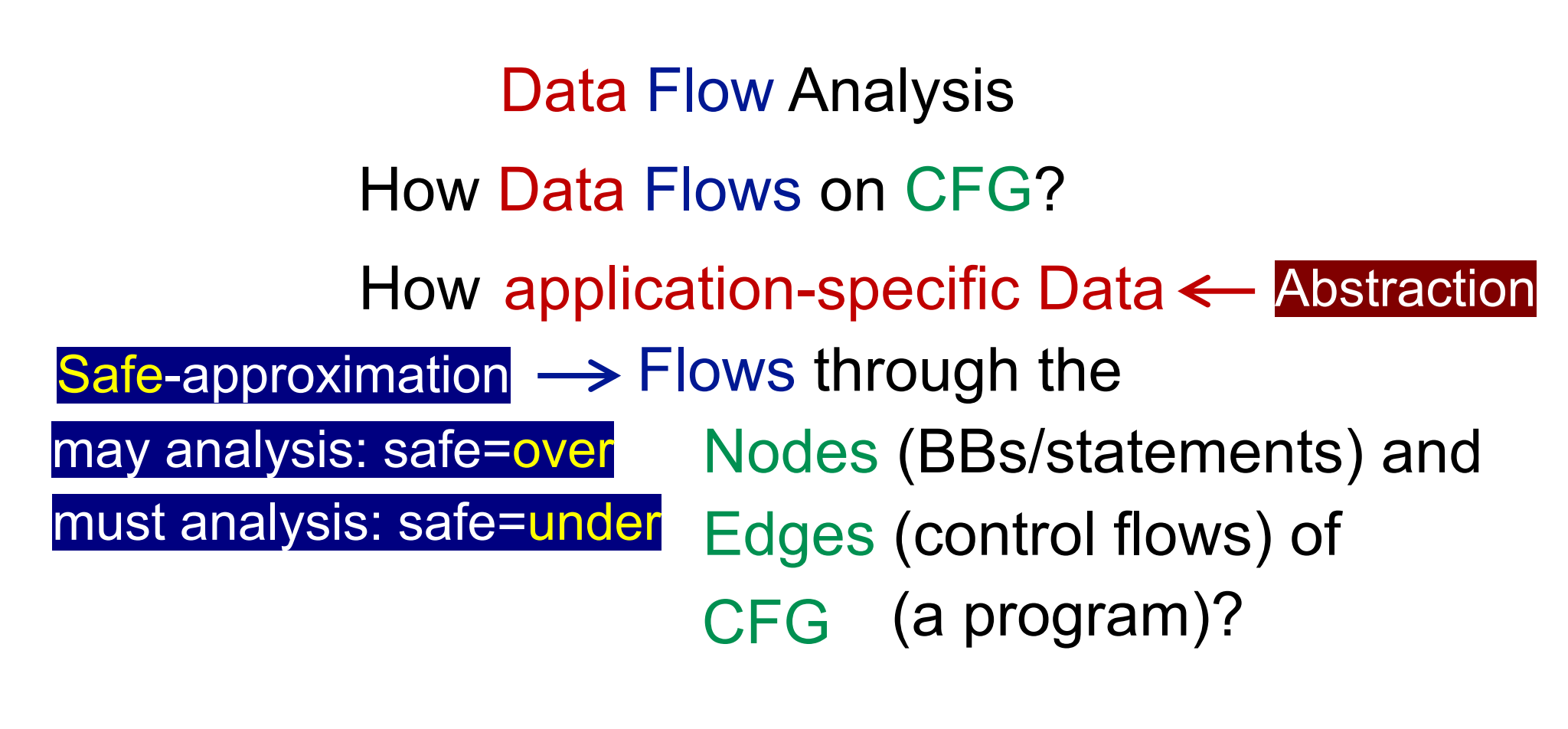
前面提到，safe-approximation的要求就是得到近似程序的行为，那要怎么做呢？

transfer function转换函数

我们通常将程序表示成图，对于一个图，包含两个要素：节点（Nodes，就是顶点Vertex）和边（Edges）。对照到程序中，节点Nodes就表示一系列的Statements组成的BasicBlock，简称为BB。边Edges就是节点之间的关系，也就是所指的Control Flow。

4

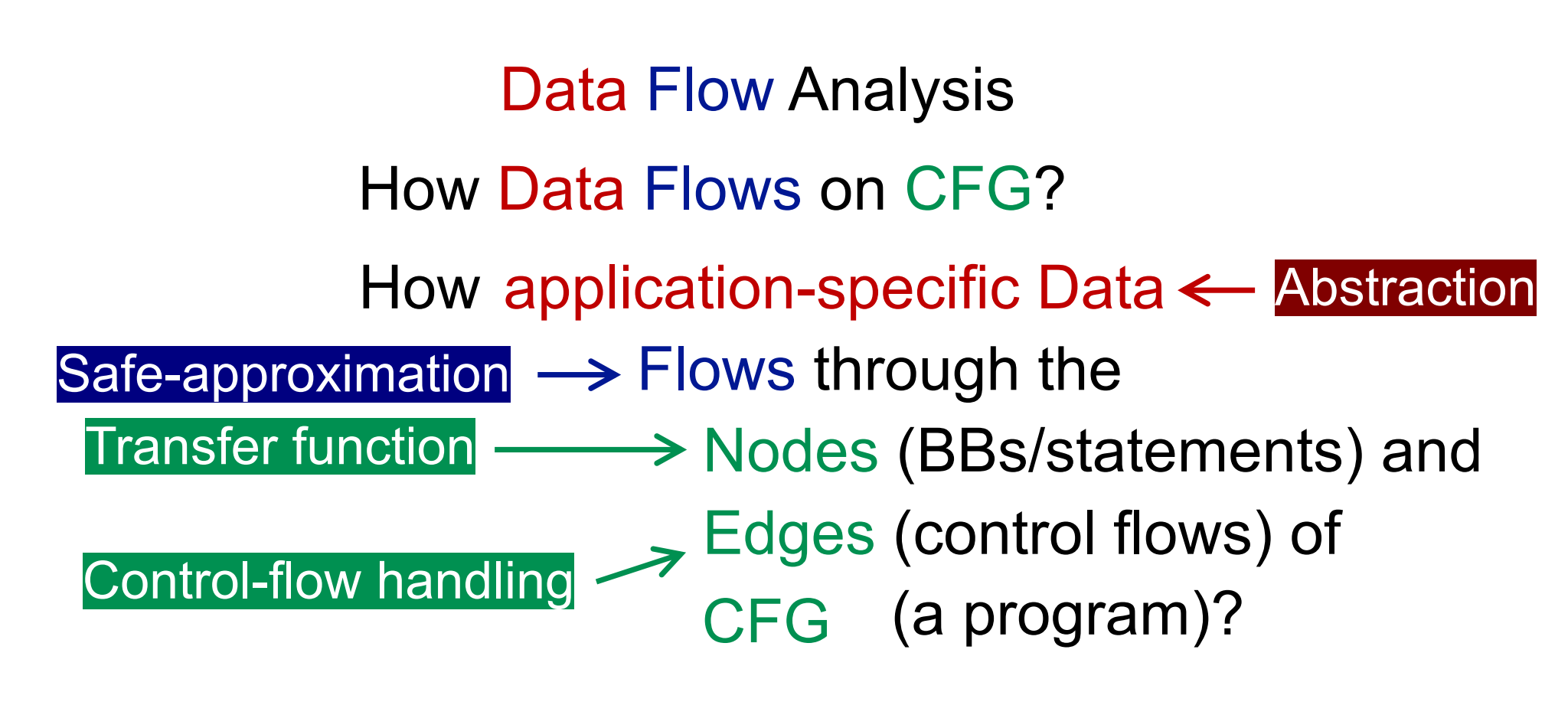
对于节点Nodes之间的转换关系，也就是Statements（BBs）和Statements（BBs）之间的转换过程，可以用一个Transfer function转换函数来表示，转换函数通常是根据程序语义和分析的目的共同设计完成。

举一个简单的转换函数的例子：

1
2
3
+ op - = -;		// 正负得负
+ op + = +;		// 正正得正
- op - = +;		// 负负得正

control-flow handling控制流处理方式

每一个节点对应一个基本块，那么每一条边就表示基本块之间流动顺序。control-flow handling就是要如何处理控制流的信息。比如前面举的x变量正负的例子，x经过分支处理之后有正有负，那在merge点要把正负都考虑进来。

6

不同的数据流分析有不同的data abstraction以及safe-approximation策略，而它们的不同也导致了有不同的转换函数（transfer function）和控制流处理方式（control-flow handling）。

基本概念

然后是学习数据流分析时必须要学习的一些最基本的符号概念。

Input and Output States输入输出状态

下图中：

  1. s1表示一个IR statement
  2. IN[s1]表示在执行s1语句之前，对应的program point的状态可以用IN[s1]表示
  3. OUT[s1]表示执行完s1语句之后，对应的program point的状态的状态用OUT[s1]来表示

7

我们知道控制流只有三种情形，顺序执行，分支和汇聚。

对于顺序执行控制流s1 -> s2有： IN[s2] = OUT[s1]

8

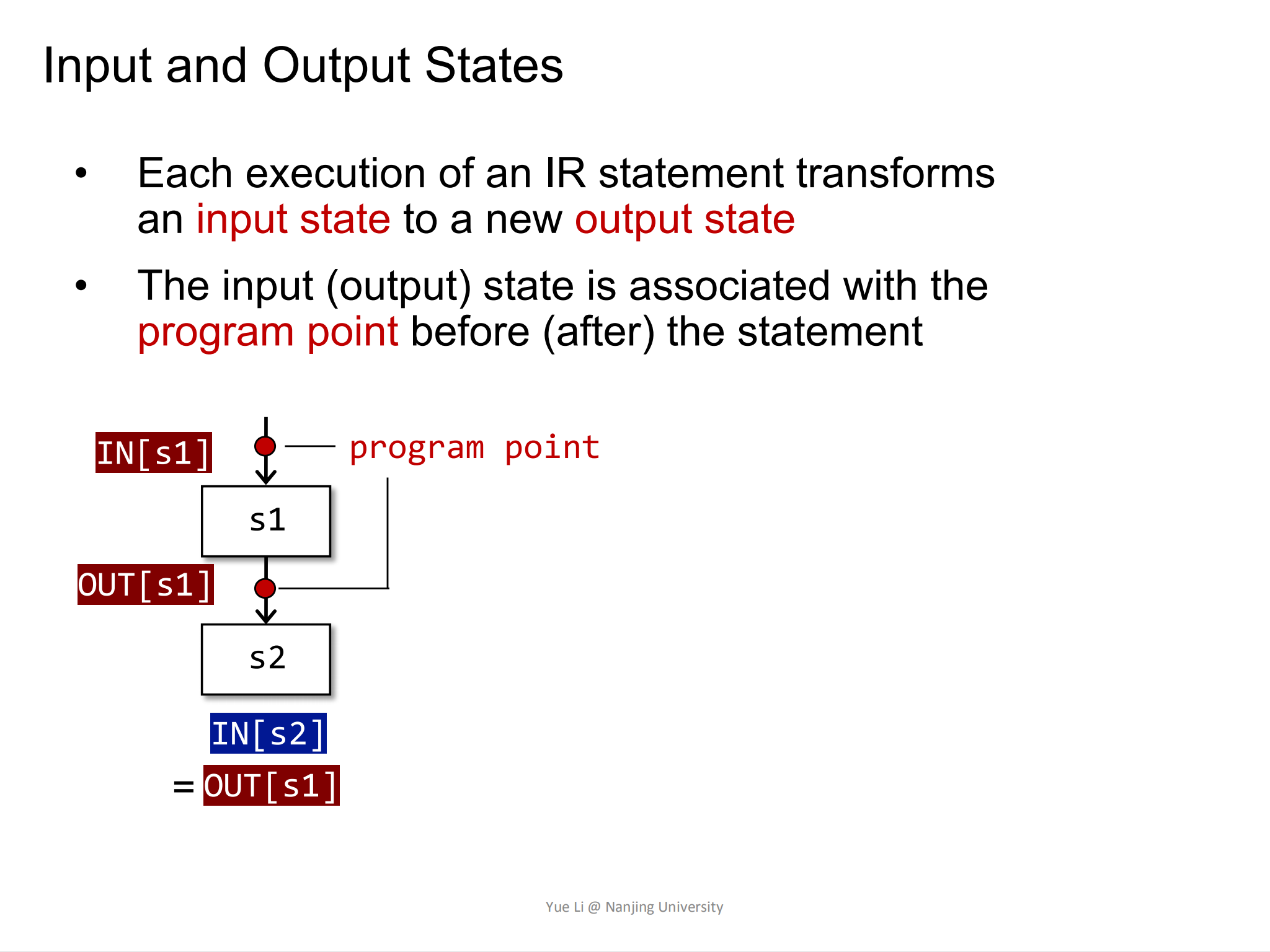
对于分支语句s1 -> s2 , s1 -> s3有：IN[s2] = IN[s3] = OUT[s1]

9

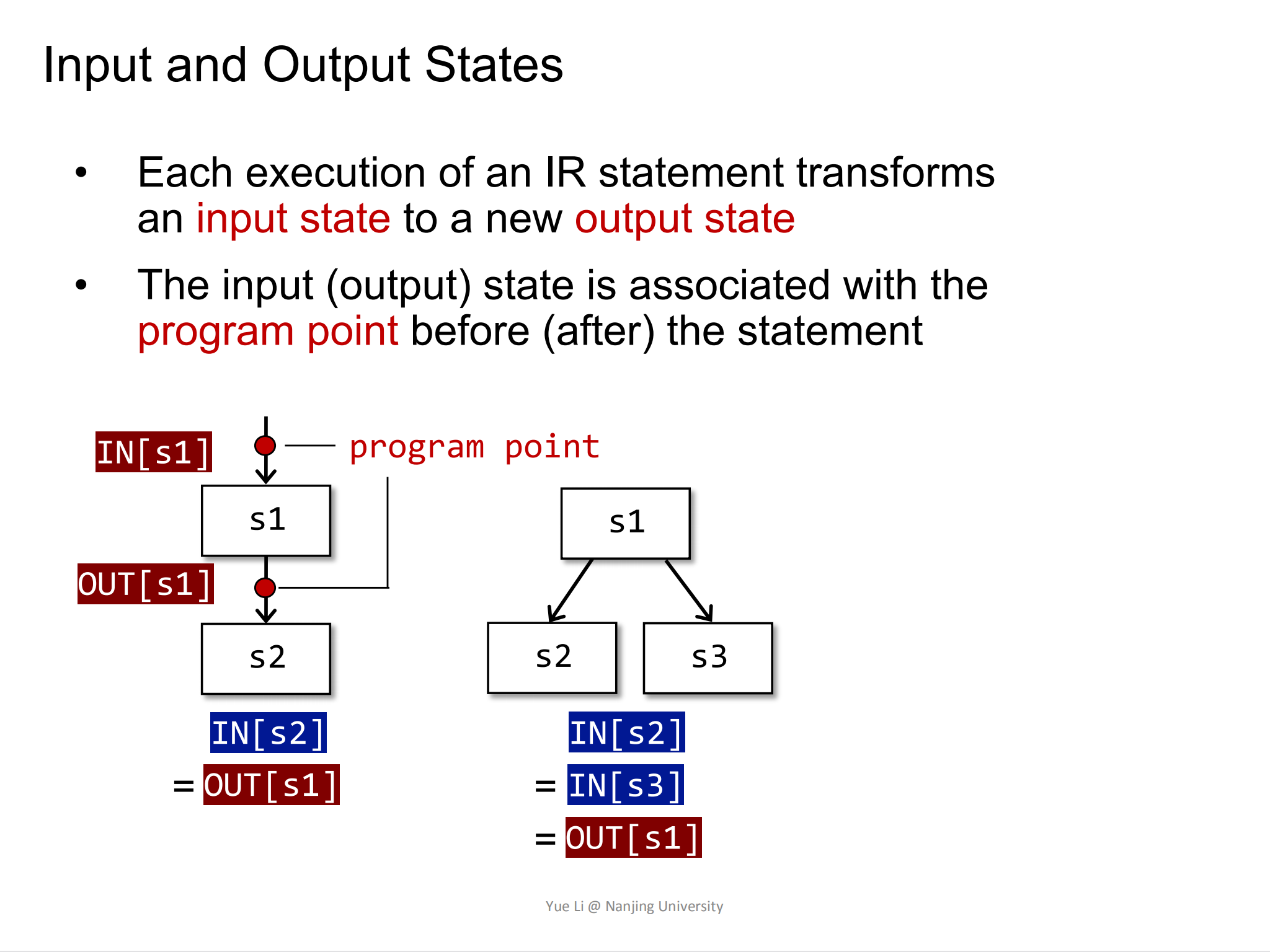
对于汇聚语句s1 -> s3, s2 -> s3有：IN[2] = OUT[s1] V OUT[s3]。其中U就是一个meet operator，并不一定表示V，也可能表示^或者其他符号，但是表达的意思就是对两个OUT[s1]和OUT[s3]同时进行处理。

10

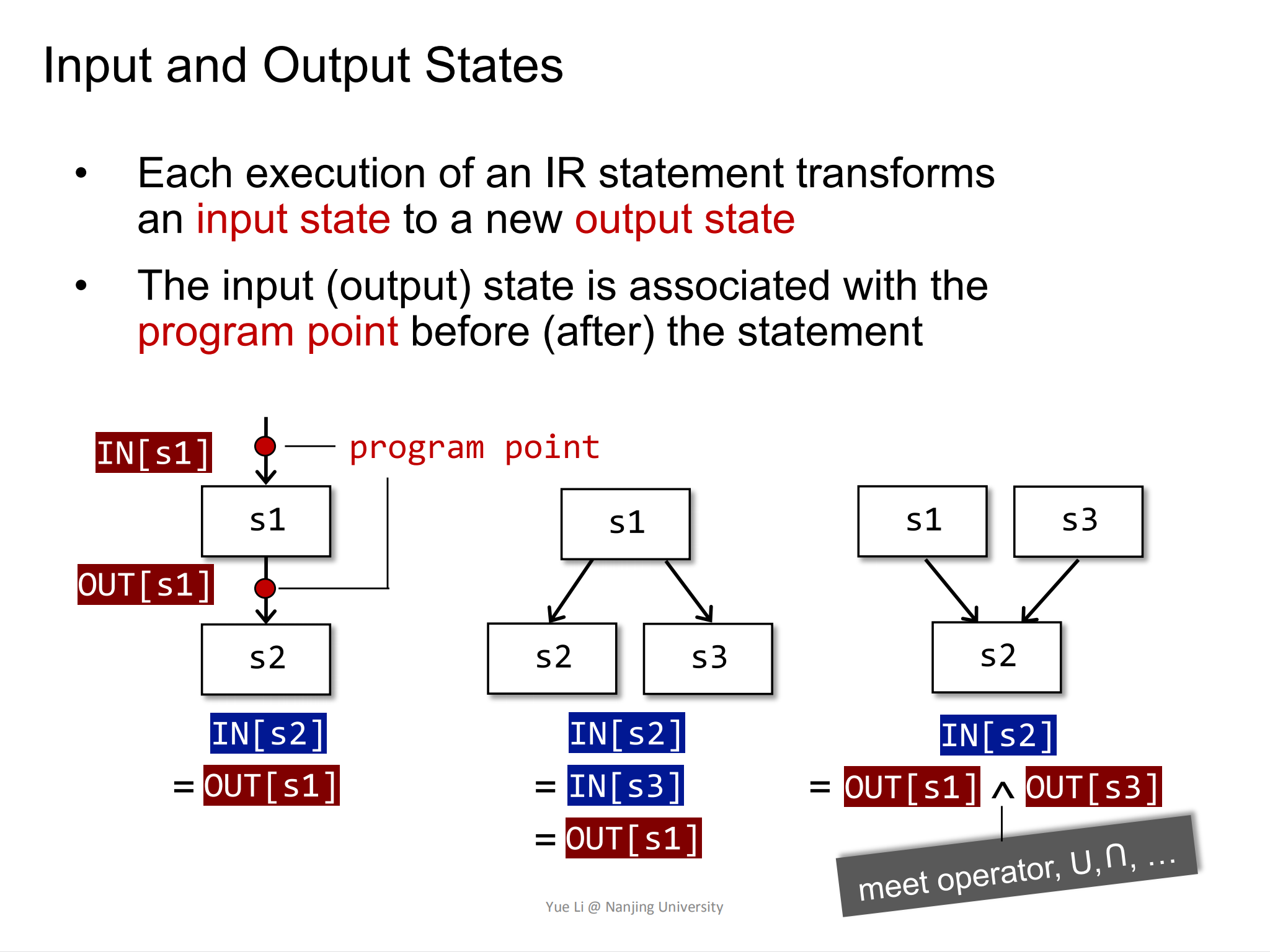
引入输入输出状态是为了什么呢？ppt中是这样阐述的：

In each data-flow analysis application，we associate with every program point a data-flow value that represents an abstraction of the set of all possible program states that can be observed for that point.

这句话的意思就是，给每一个program point（程序点），关联一个数据流的值（data-flow value），这个值代表了关于program states（程序状态）的抽象集合，即program states在一个program point的所有的可能值的一个抽象，作为static analysis的结果。

比如下图ppt中，红框有一段简单的代码，每个statement后有一个红点表示一个program point。

绿框中则记录了执行完一条statement之后，x和y的状态（比如正，负，是否定义）。绿框就是对每个program point分析的一个结果。当然，我们在绿框的结果中加入更多的信息，比如x=10，y=undefined等等。另外，该抽象集合还有一个值域domain，数据流值（data-flow value）就限制在值域domain中。

11

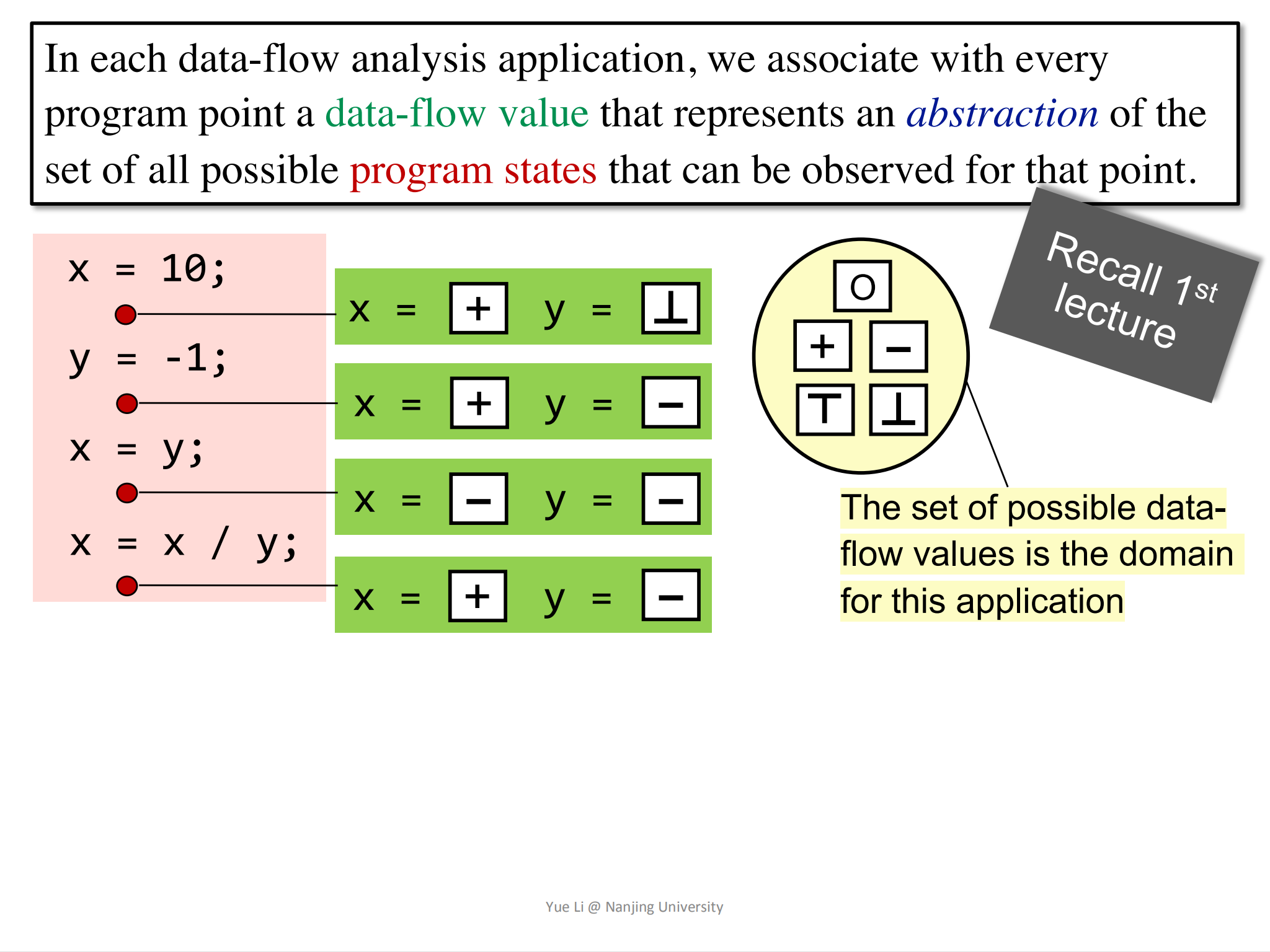
data-flow analysis概念

到这里就可以给出一个关于data-flow analysis的总体概览。data-flow analysis就是为程序中所有的statements的in和out找到一个solution，主要是通过解析一系列的safe-approximation约束。这些约束就是transfer function和control flow信息。也就是说，通过不断解析这些转换函数和控制流信息的约束规则，就会得到一个solution，该solution会给每一个statements的in/out program point关联一个data flow value。

12

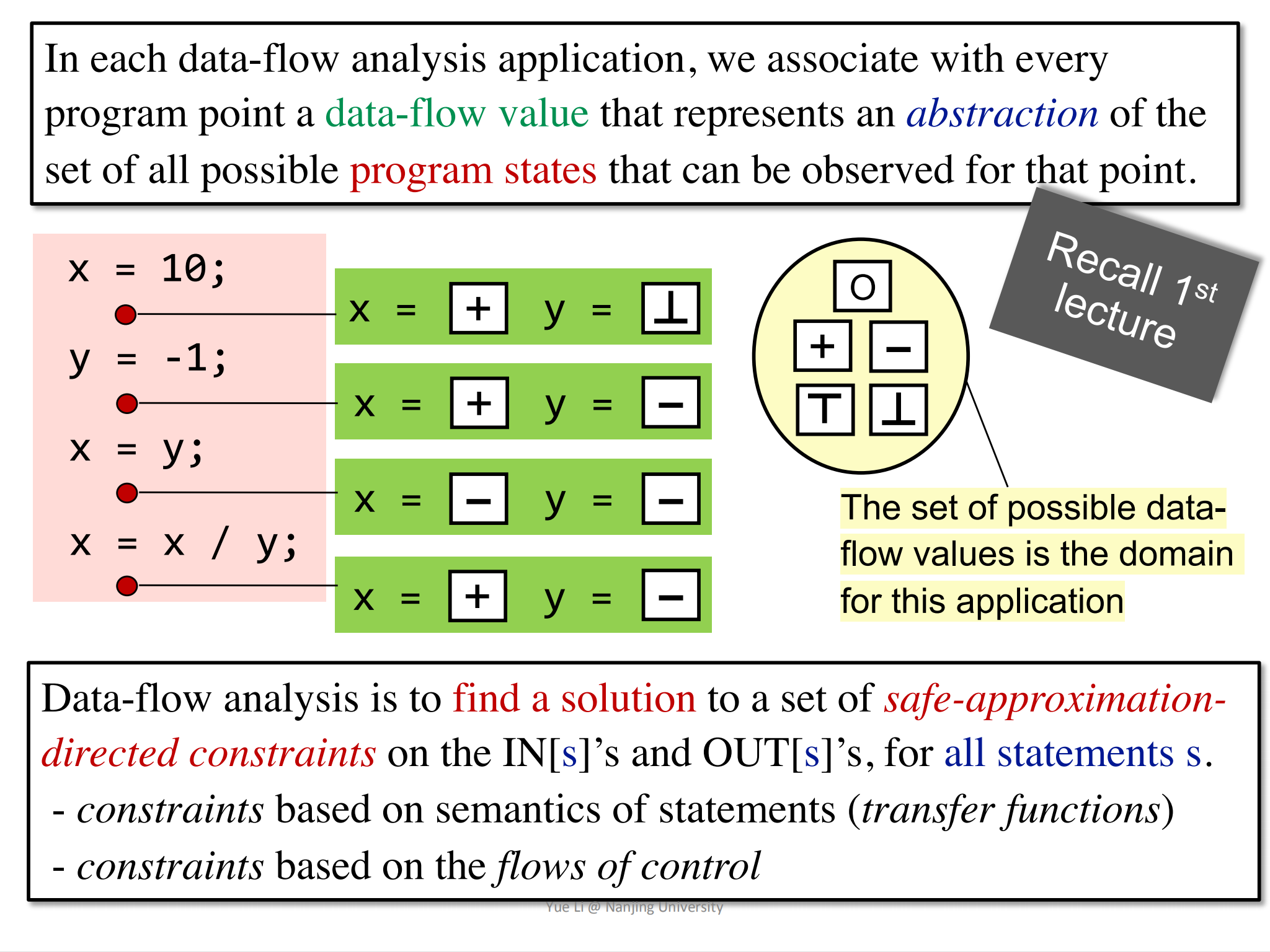
Transfer Function’s Constraints

当我们沿着控制流的方向进行分析时，此时叫做前向分析：

13

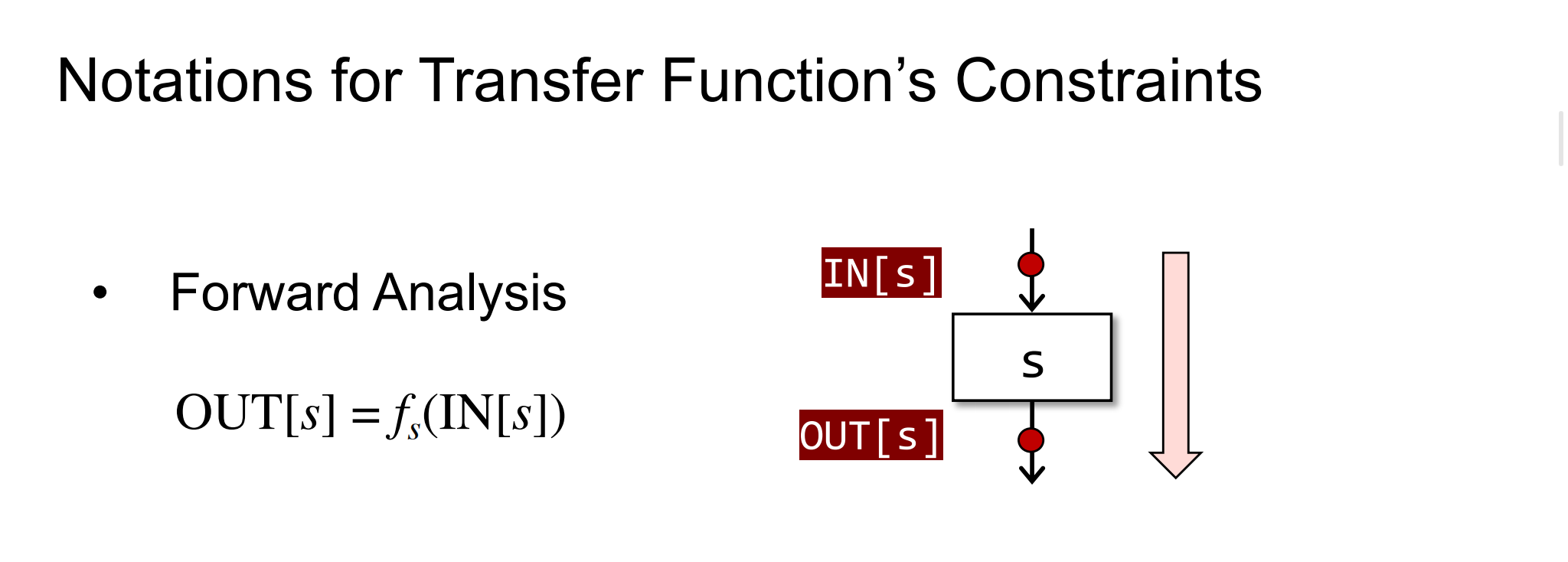
上图中transfer function的意思就是，将IN[s]通过转换函数fs转换为OUT[s]。

如果我们分析时，沿着控制流反向分析，则有：

14

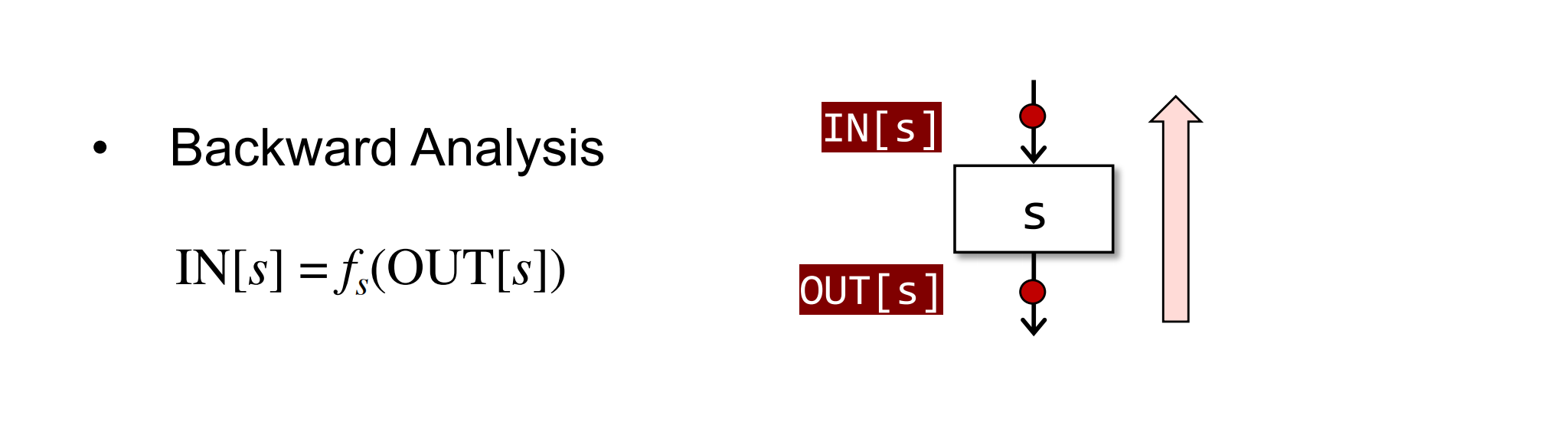
有时候，进行backward analysis的时，会对control flow进行反向建模，相当于到达一个forword的效果。

Control Flow’s Constraints

根据基本块BasicBlock的特点，我们可以将控制流分为BasicBlock之间和BasicBlock之内。

对于BasicBlock内部的Statements，上一条statement的输出out就是这条statement的输入in，用符号来表示它们之间的in和out关系有：

15

对于整个BasicBlock而言，它的输入in就是第一条statement的输入in，它的输出就是最后一条输出out。但对于BasicBlock和BasicBlock之间来看，它的in和out是这样的：

16

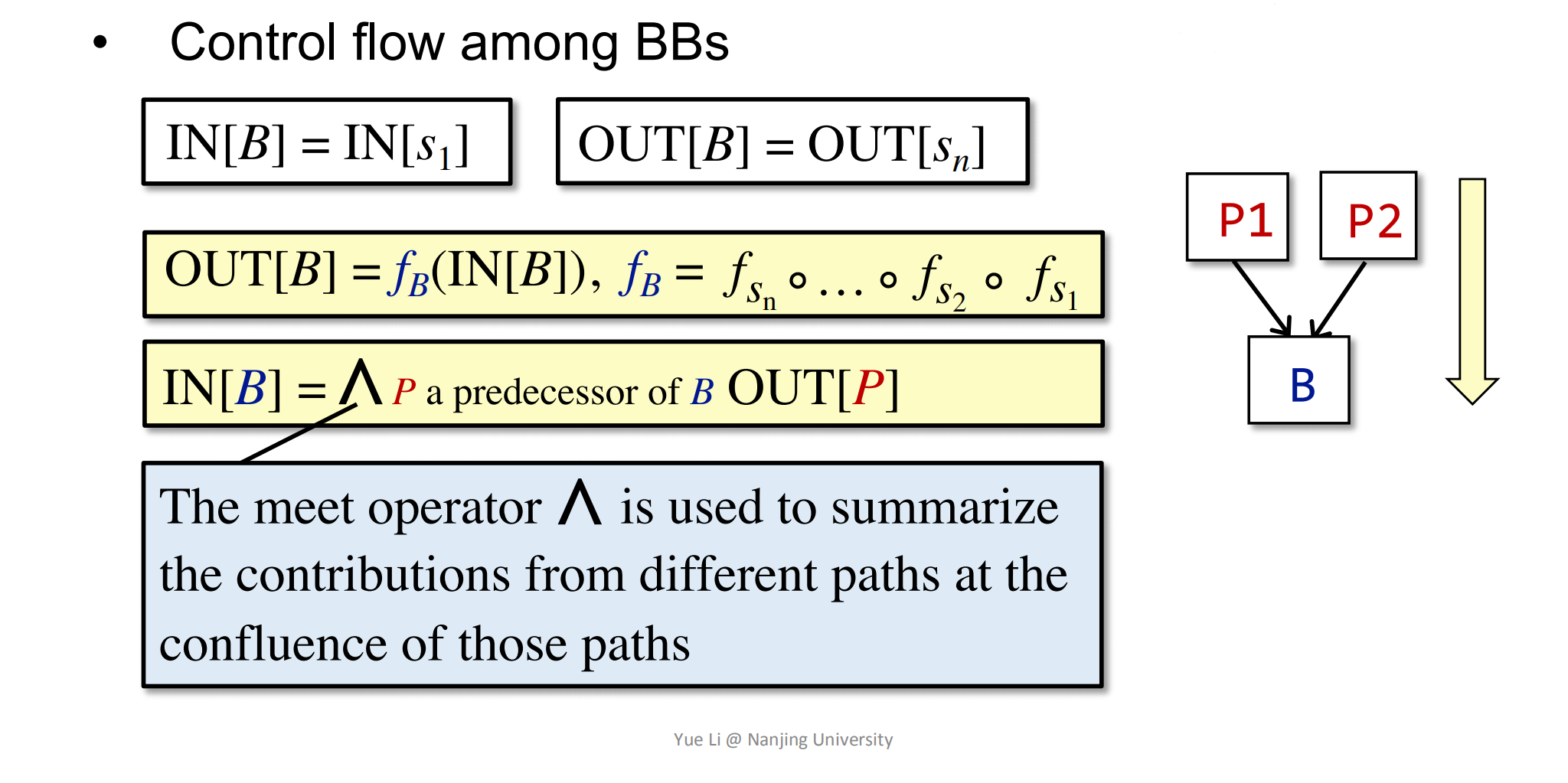
其中fb表示是经过了BasicBlock块内多个转换函数最后得到的转换函数fb。

IN[B]等于将所有的OUT[P]汇总起来后的结果（P是B的前驱节点）。上图中的meet operator^就是表示在汇聚点，通过一定处理，将OUT[P]组合起来作为IN[B]。

当进行backward analysis的时候，则有：

17

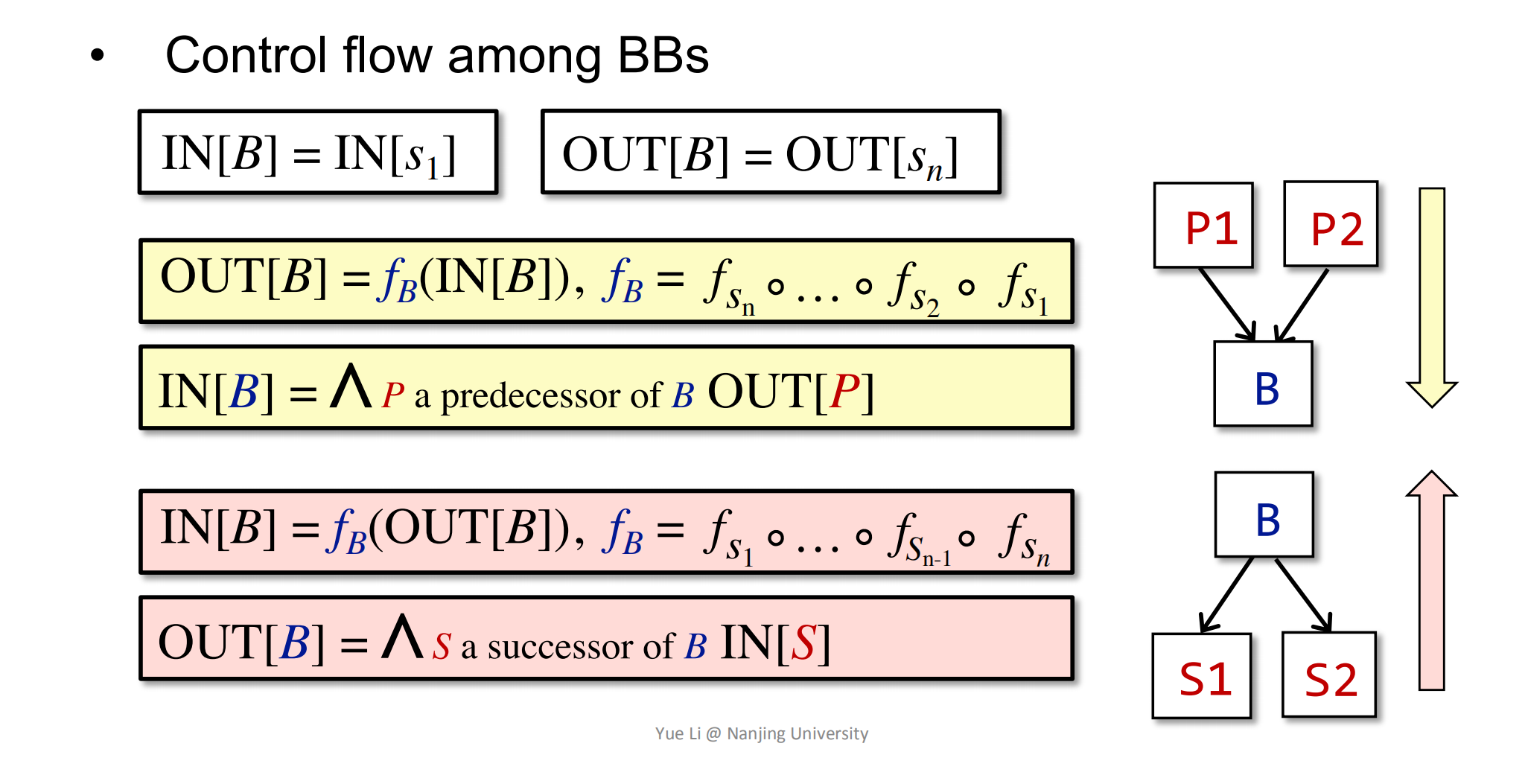
Reaching Definitions Analysis

什么是Reaching Definitions

Reaching Definitions Analysis即可达定义分析，是编译优化中常用的分析手段。

可达性定义：

A definition d at program point p reaches a point q if there（这是一个may analysis） is a path from p to q such that d is not “kill” along that path.

即在程序点p的一个定义d，到程序点q是可达的，当且仅当这个定义d在从程序点p到程序点q这条路径不会被kill掉。

这个变量v的定义d指的是为这个变量分配数值的statements，比如初始化和赋值。比如下图，变量v在程序点p被定义，在从程序点p到程序点q，变量v不会被重新定义，那就可以说，程序点p的定义d到程序点q是可达的：

18

可达定义分析除了用于编译优化，还可以用在其他的地方，比如未定义变量检测。我们知道CFG中有一个entry node和exit node，现在在entry node中为所有变量添加一个dummy definition。如果假设在程序点p，发现变量v被使用了，并且变量v在程序点p是一个可达定义，那么有可能就发生了“使用未定义的变量”错误，但是也可能没有，因为变量v在其他的path上有新的定义，那才是一条程序在运行时会走的路径。

Reaching Definitions表示

程序中所有变量的definitions可以用一个bit vectors来表示，比如一个程序中有100个definition，但是这里要注意，并不是表示有100个变量：

D1, D2, D3, D4, …, D100 = 000…0

可达定义分析是一种safe-approximation，主要从两个方面入手：转换函数和控制流信息。

比如现在有一个definition d为：

1
D: v = x op y

这条statement为变量v “生成了”一个definition D，并且这个definition D kill掉了程序中所有定义的v，其他变量的定义则不受影响。

Transfer Function

我们用BasicBlock来表示这条statement，那么可以得到相应的转换函数为：

19

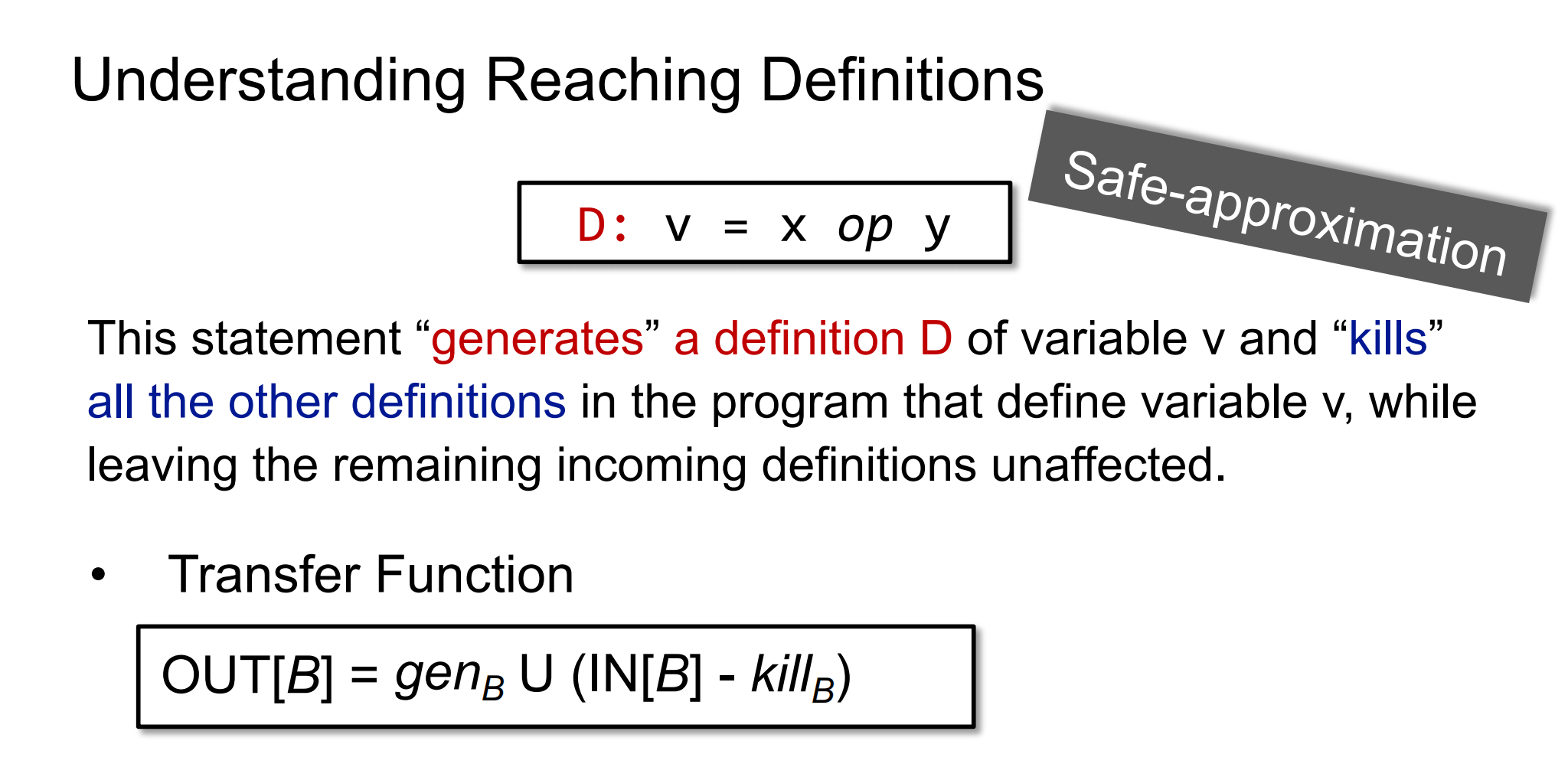
其中：

gen[B]表示新生成的定义;

IN[B]表示流进当前Block的定义；

kill[B]表示去除的其他地方的定义；

OUT[B]表示从该Block流出的定义。

以下图为例，现在有7个定义（d1, d2, d3, d4, d5, d6, d7）。B1中对3个不同的变量（i, j, m）有3个定义，所以gen[B1] = { d1, d2, d3 }，同时，其他对变量（i, j, m）的定义都要被kill掉，所以kill[B1] = { d4, d5, d6, d7 }。

20

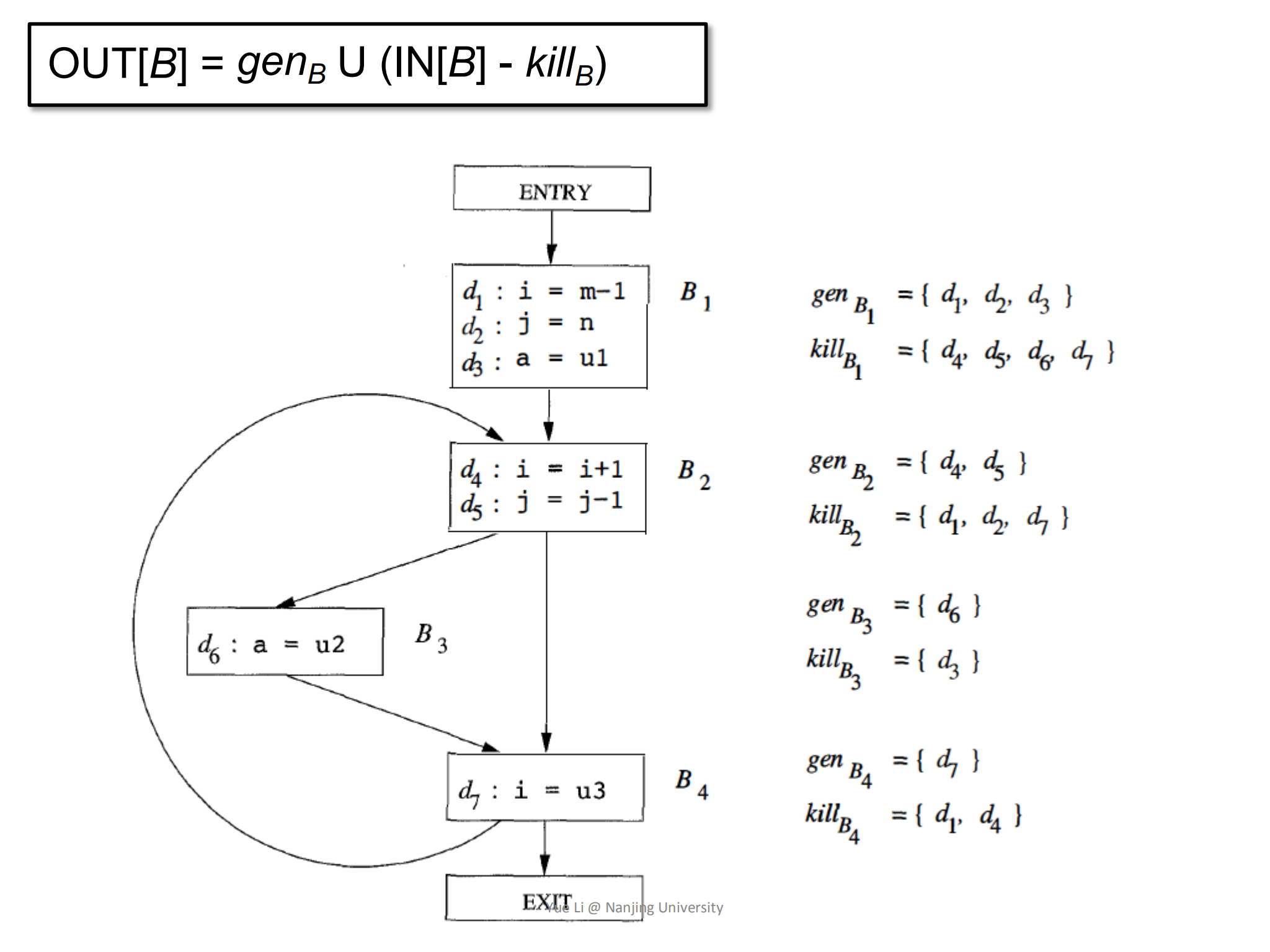
Control Flow

针对control flow则有：

21

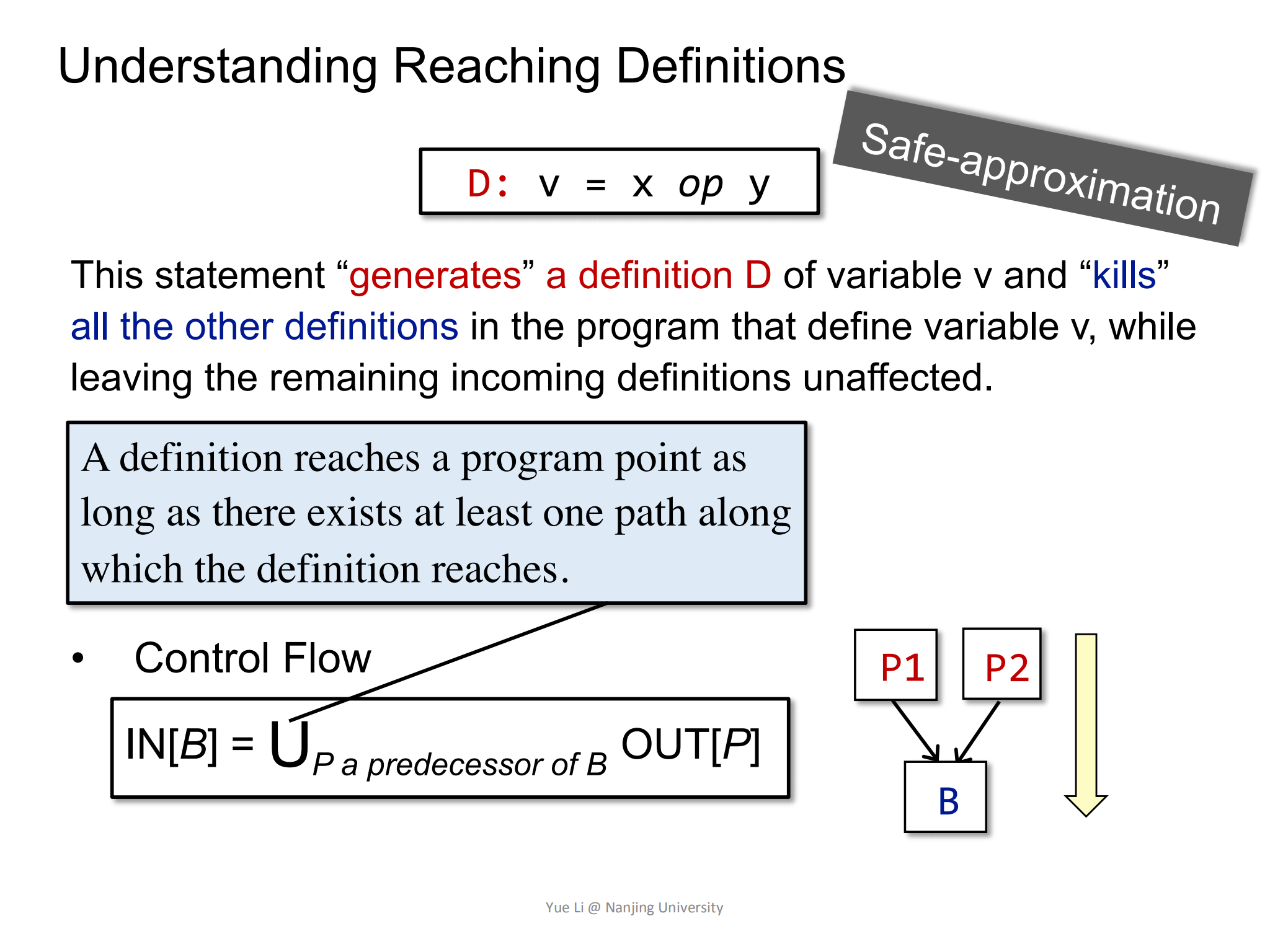
这里IN[B]是所有BasicBlock B的前驱P的OUT[P]总和，因为要做一个over-approximation，所以每一条path都要考虑到，所以对应的符号是U。

Reaching Definitions迭代算法

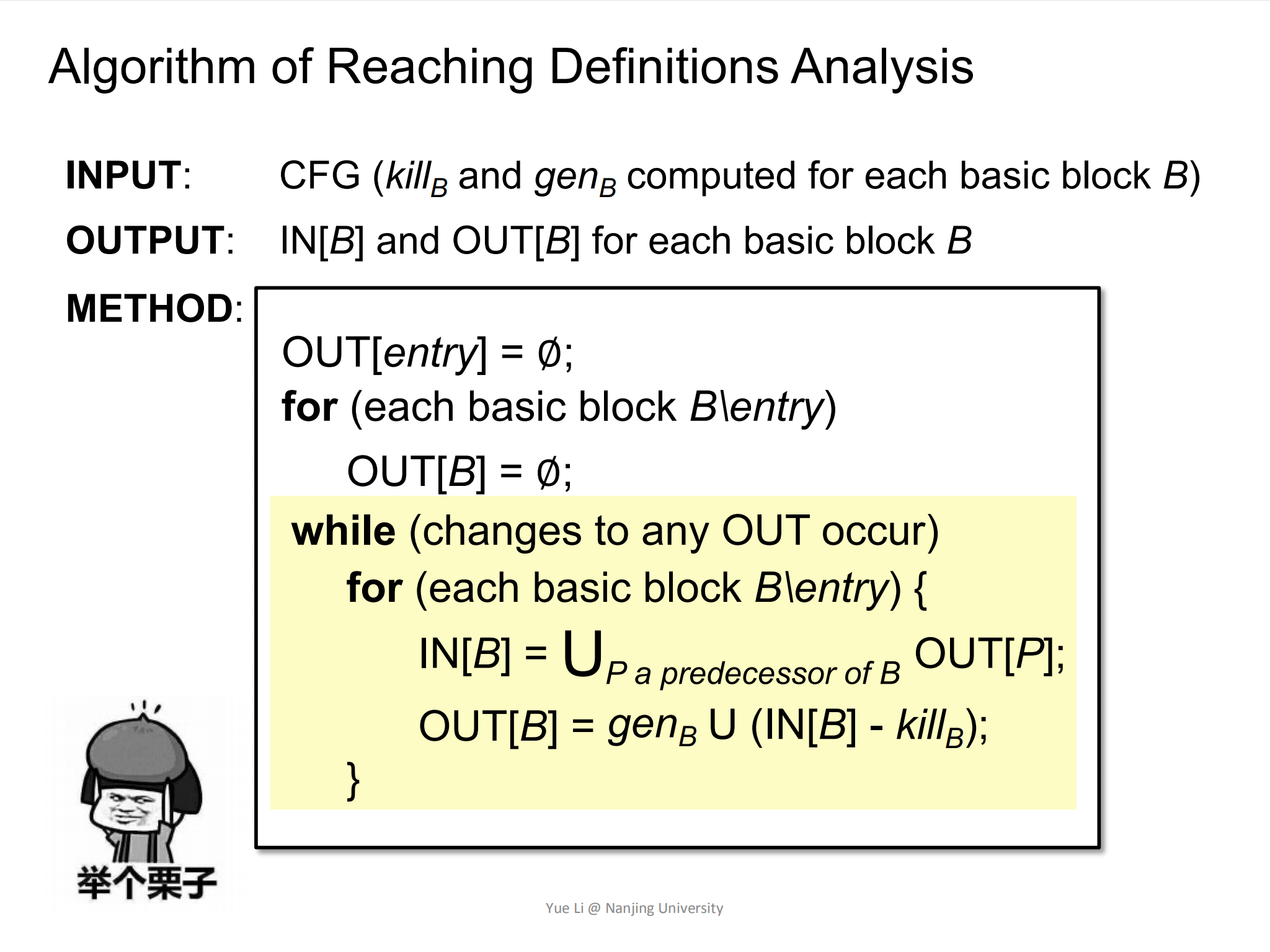
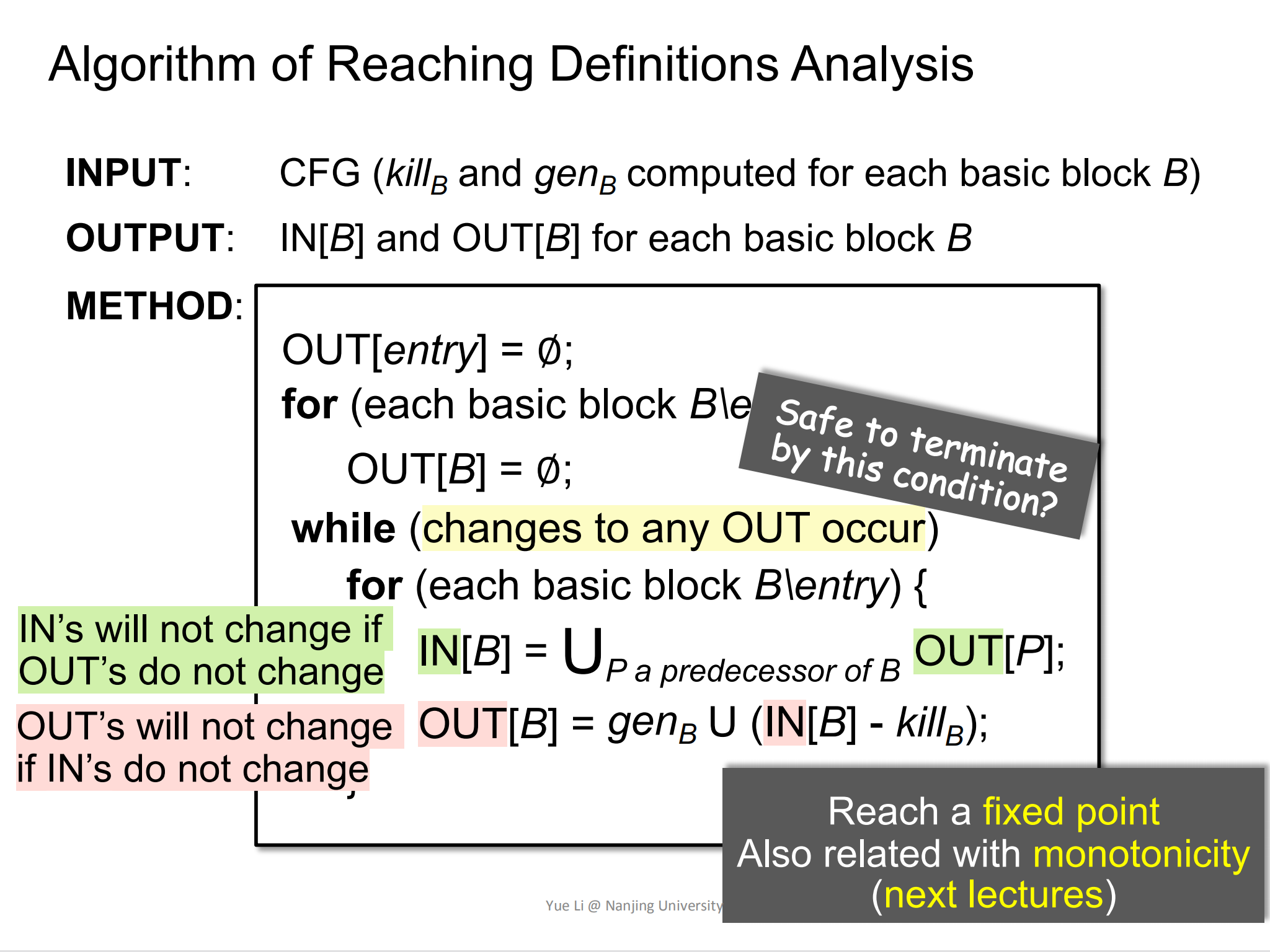
可达定义迭代算法如下图所示：

44

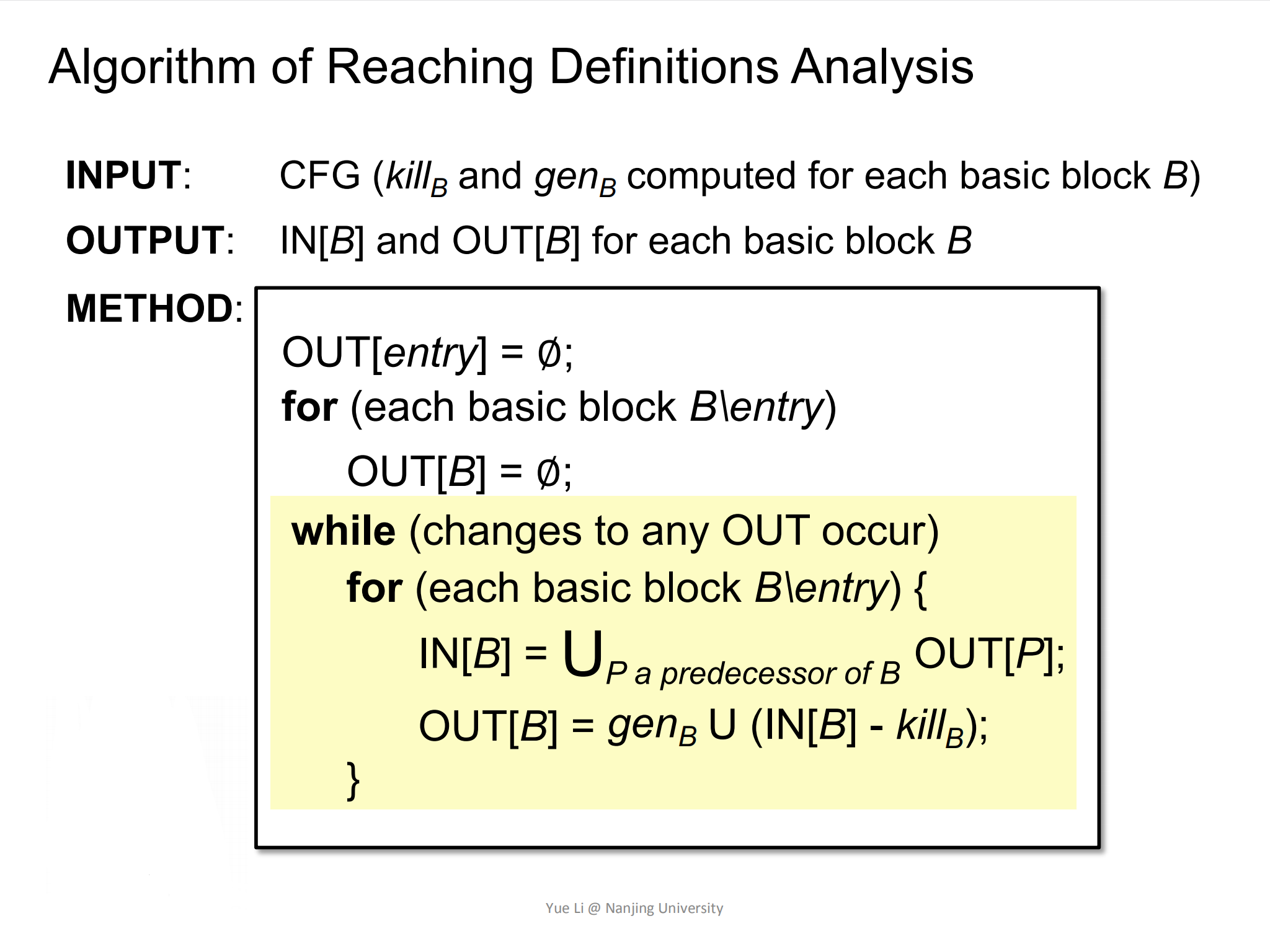
  1. 首先，先将OUT[entry]清空，这个OUT[entry]也被称为boundary condition（边界值）；
  2. 然后，将除了entry块的BB块的OUT[B]也清空。既然都是清空的初始化行为，为什么不放在一起呢？因为这个算法是一个经典的迭代算法模板，一个模板不应该仅对over-approximation中的reaching definition迭代适用，也应该对其他的data-flow analysis的迭代算法也适用。在一些data-flow analysis中，它的边界值可能和其他的BB不一样，比如在must analysis中，OUT[entry]=∅，而OUT[B\entry]则不是。
  3. 然后为B\entry块分别计算IN[B]和OUT[B]；
  4. 最后，迭代是否结束的信号取决于：是否有BasicBlock的OUT发生了变化。

Reaching Definitions算法实例

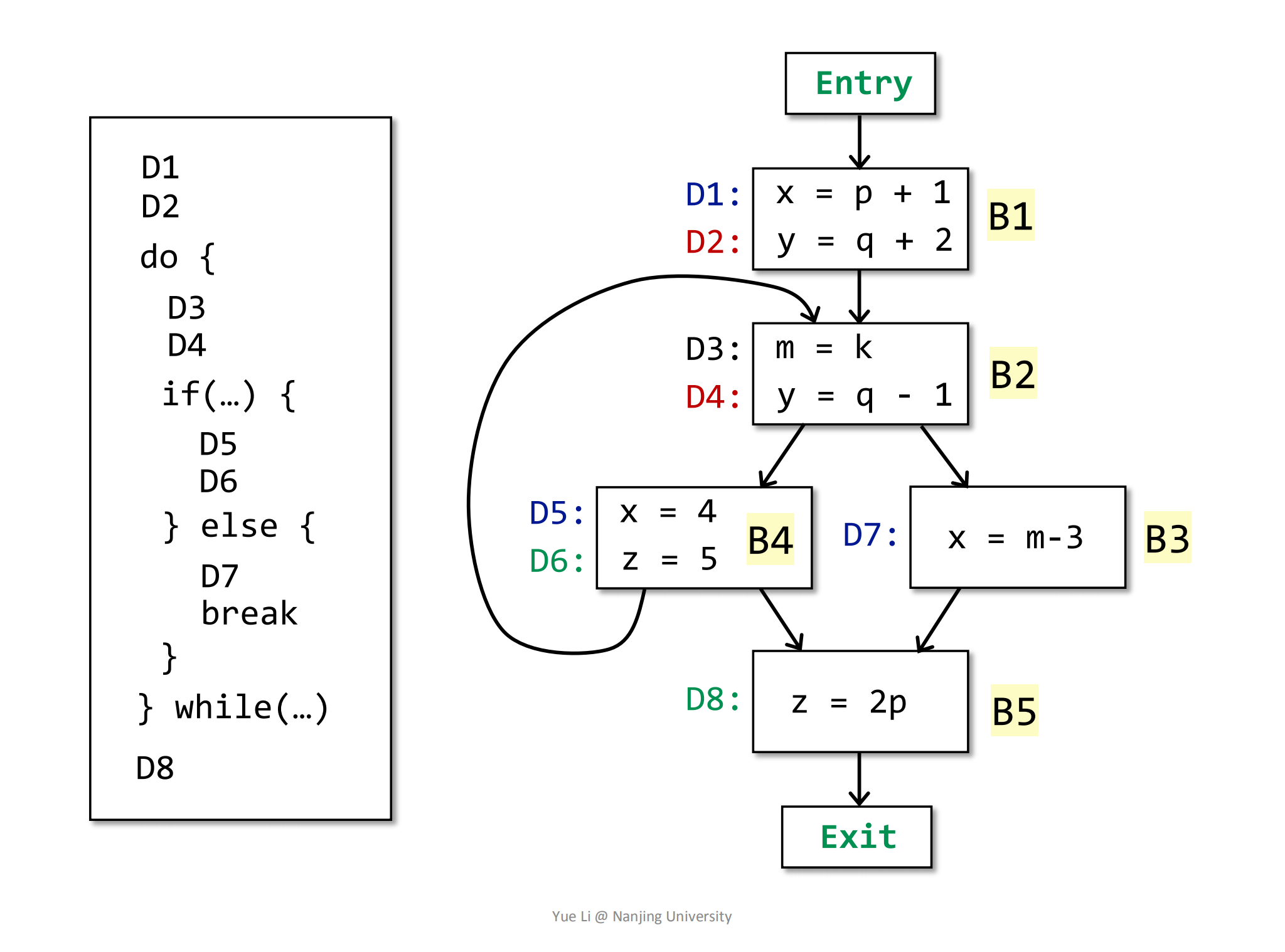
比如现在有这样一个控制流，左边对应的是它可能的语句。这个控制流被分为5个基本块（B1，B2，B3，B4，B5）和5个变量（x，y，z，m）分别用不同的颜色表示。这里5个基本块一共对应了8个definition：

22

根据迭代算法的初始步骤，会将OUT[entry]和其他BB块的OUT[B]设置为∅：

1
2
3
4
OUT[entry] = ∅;
// B\entry 表示BasicBlock去除entry块
for (each basic block B\entry)
	OUT[B] = ∅;

初始化后，每一个BB块的IN和OUT结果都表示为：

1
2
D1 D2 D3 D4 D5 D6 D7 D8
0  0  0  0  0  0  0  0

23

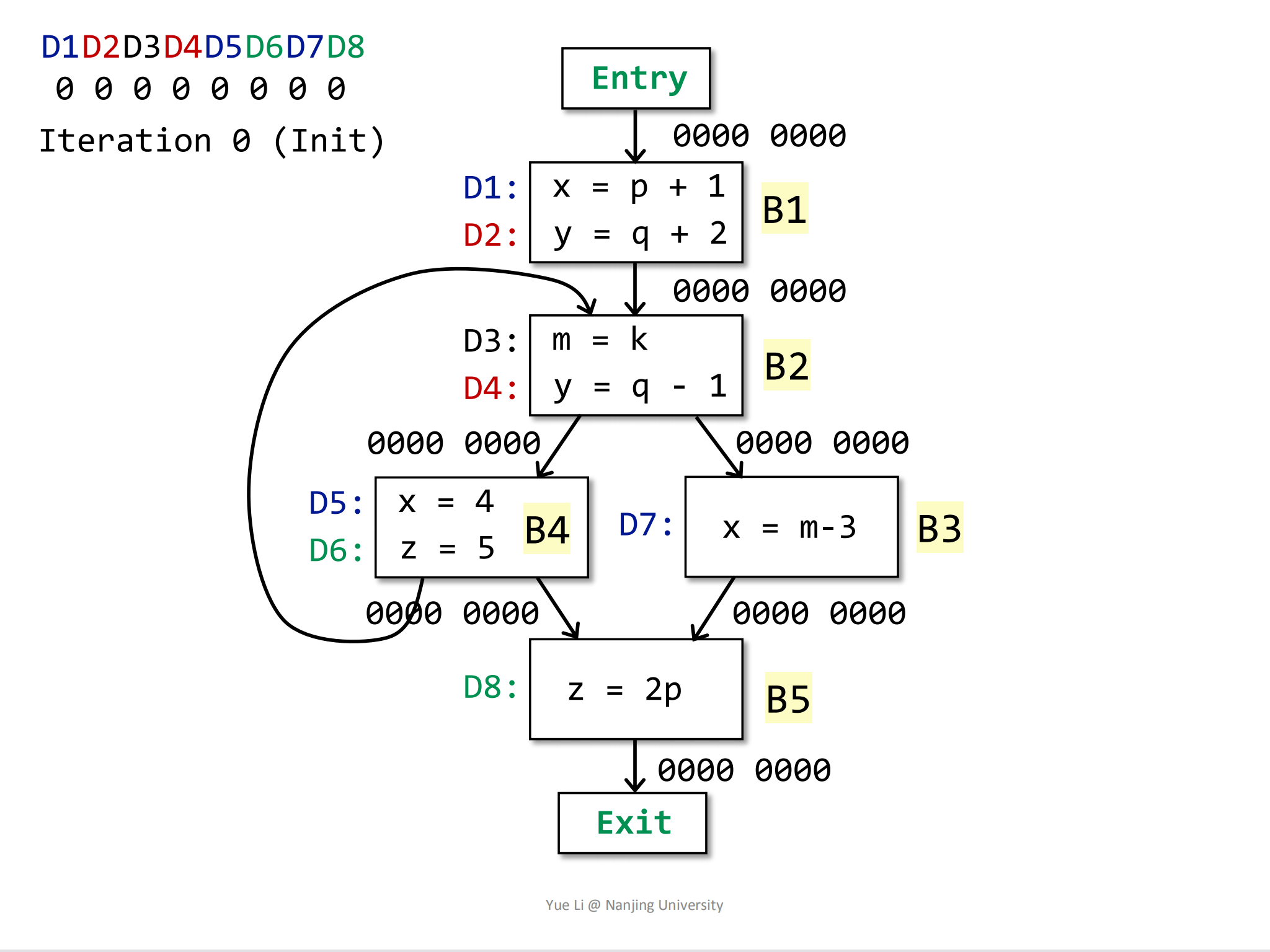
要注意这个0000 0000结果是作用在每一个program point上的，而不是直接作用在BB块上。

然后开始迭代部分：

24

第一轮迭代

  1. 第一次迭代首先作用在B1块上，首先是IN：

    1
    IN[B1] = 0000 0000

    然后计算OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B1] = = { D1, D2 } = 1100 0000
    IN[B1] = 0000 0000
    kill[B1] = { D4, D5, D7 } = 0001 1010

    OUT[B1] = gen[B1] U (IN[B1] - kill[B1])
    		= 0000 0000 - 0001 1010 = 0000 0000
    		= 1100 0000 U 0000 0000
    		= 1100 0000

    现在得到的结果是：

    1
    2
    IN[B1]  = 0000 0000
    OUT[B1] = 1100 0000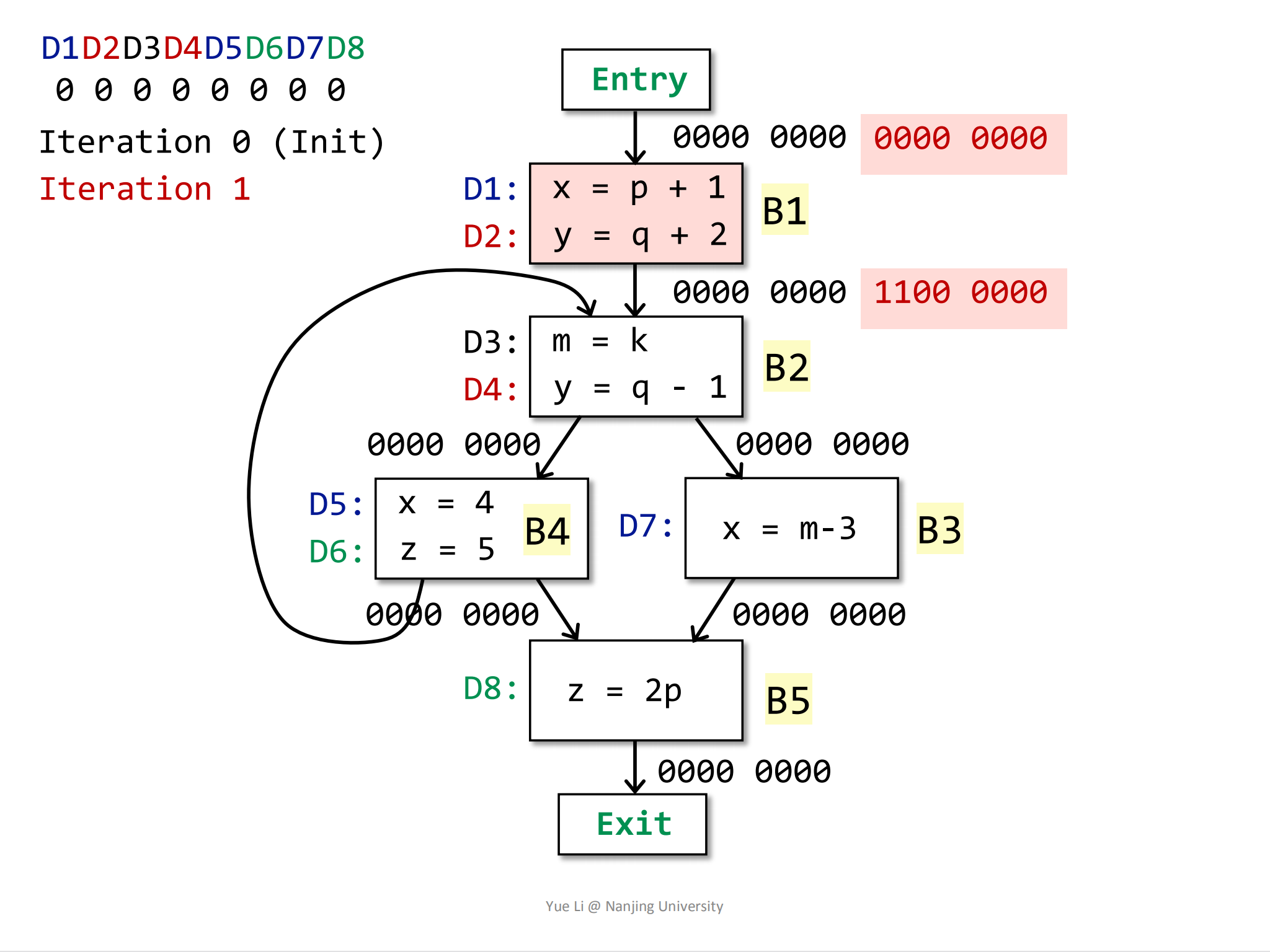

    25

  2. 然后是针对B2，B2的IN有分别来自B1和B4，所以得到IN[B2]为：

    1
    2
    3
    IN[B2] = OUT[B1] U OUT[B4]
    	   = 1100 0000 U 0000 0000
    	   = 1100 0000

    然后求解B2的OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B2] = { D3, D4 } = 0011 0000
    IN[B2] = 1100 0000
    kill[B2] = { D2 } = 0100 0000

    OUT[B2]  = gen[B2] U (IN[B2] - kill[B2])
    		 = 0011 0000 U (1100 0000 - 0100 0000)
    		 = 0011 0000 U 1000 0000
    		 = 1011 0000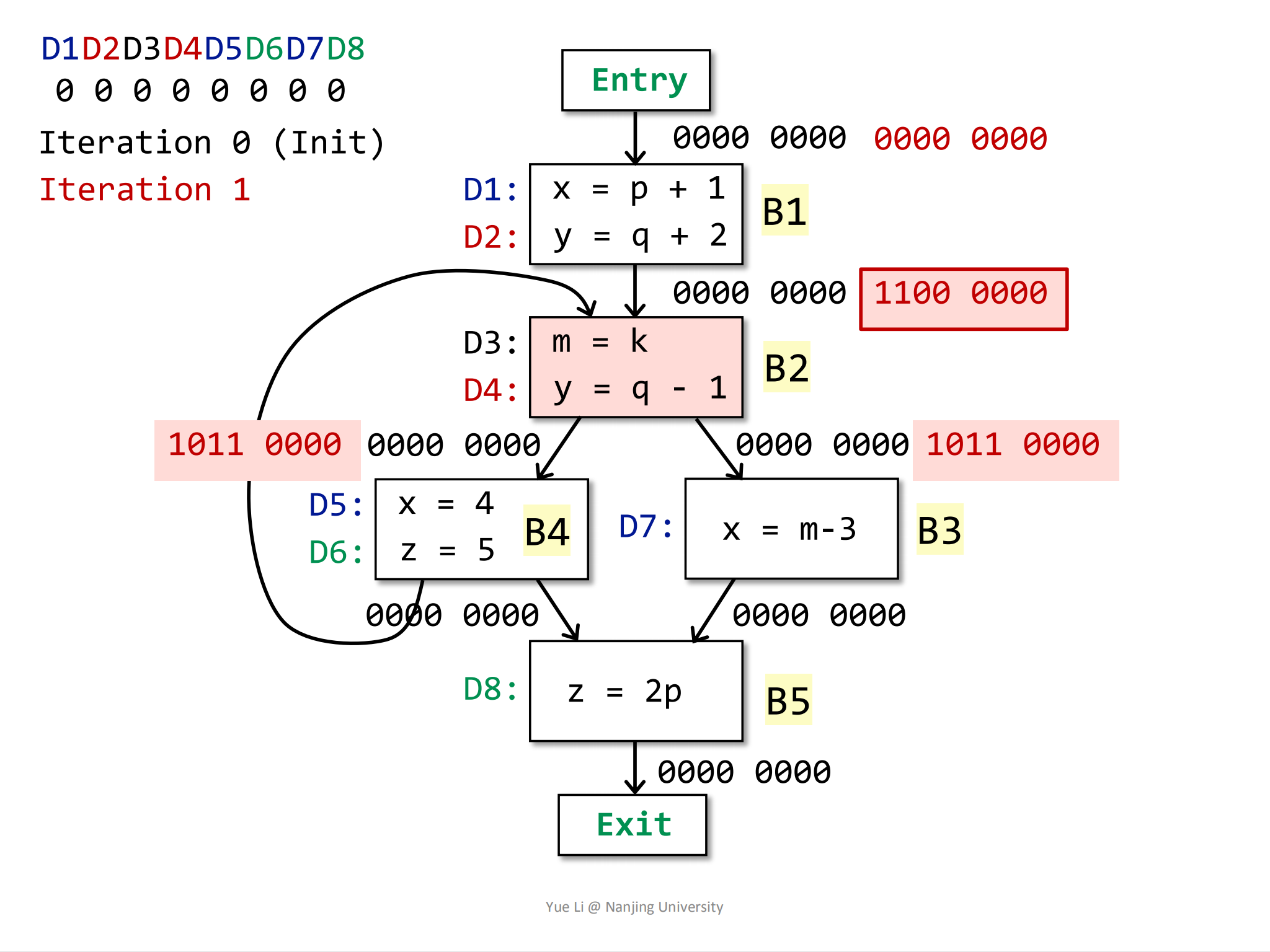

    26

  3. 接着是B3的IN，就是来自B2的OUT：

    1
    2
    IN[B3] = OUT[B2]
    	   = 1011 0000

    然后计算OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B3] = { D7 } = 0000 0010
    IN[B3] = 1011 0000
    kill[B3] = { D1, D5 } = 1000 1000

    OUT[B3] = gen[B3] U (IN[B3] - kill[B3])
    		= 0000 0010 U (1011 0000 - 1000 1000)
    		= 0000 0010 U 0011 0000
    		= 0011 0010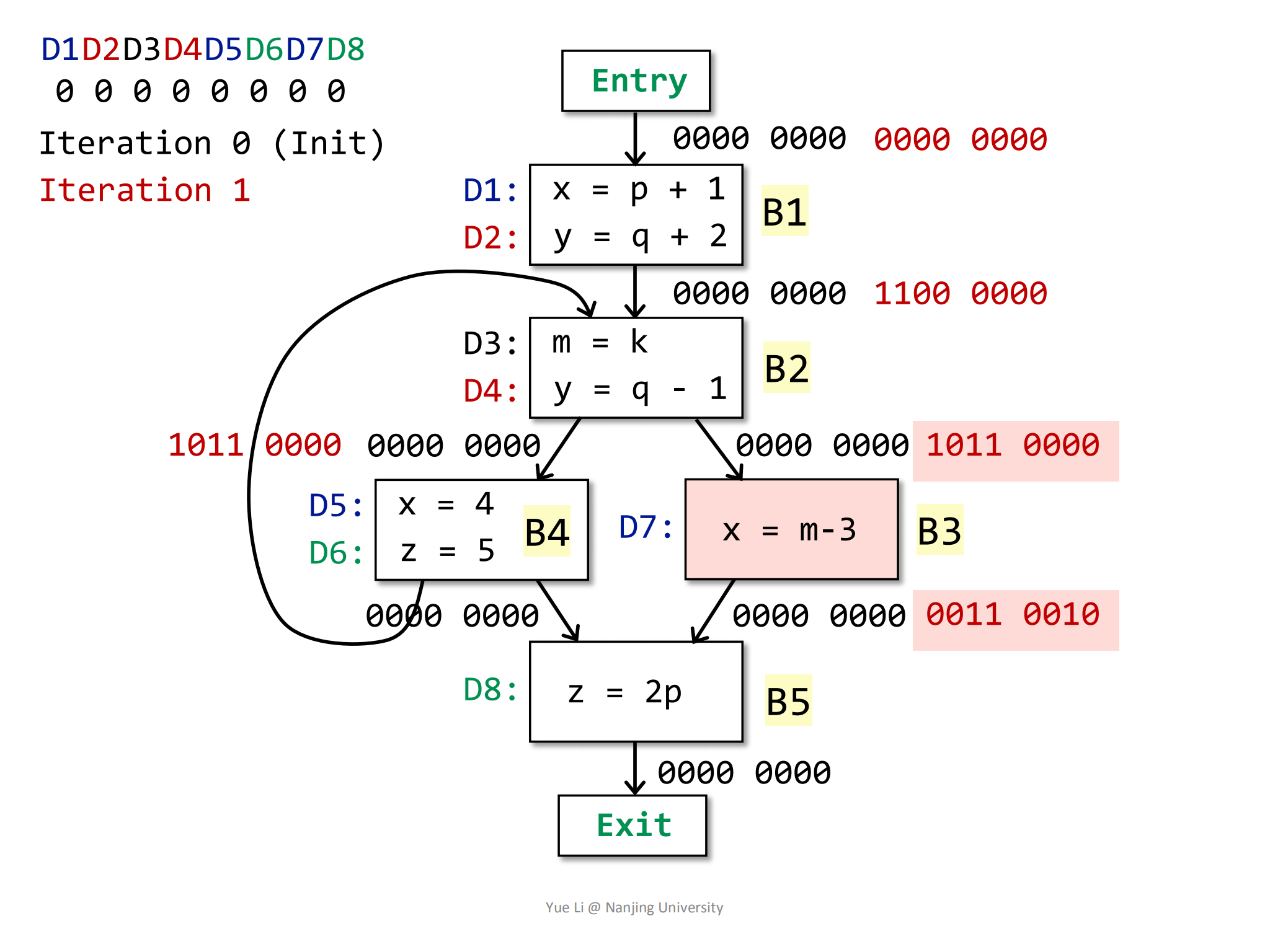

    27

  4. 然后是B4块的IN，即为IN[B2]：

    1
    2
    IN[B4] = IN[B2]
    	   = 1011 0000

    接着计算OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B4] = { D5, D6 } = 0000 1100
    IN[B4] = 1011 0000
    kill[B4] = { D1, D7, D8 } = 1000 0011

    OUT[B4] = gen[B4] U (IN[B4] - kill[B4])
    		= 0000 1100 U (1011 0000 - 1000 0011)
    		= 0000 1100 U 0011 0000
    		= 0011 1100

    同时需要注意的是，B4的OUT也是B2的IN：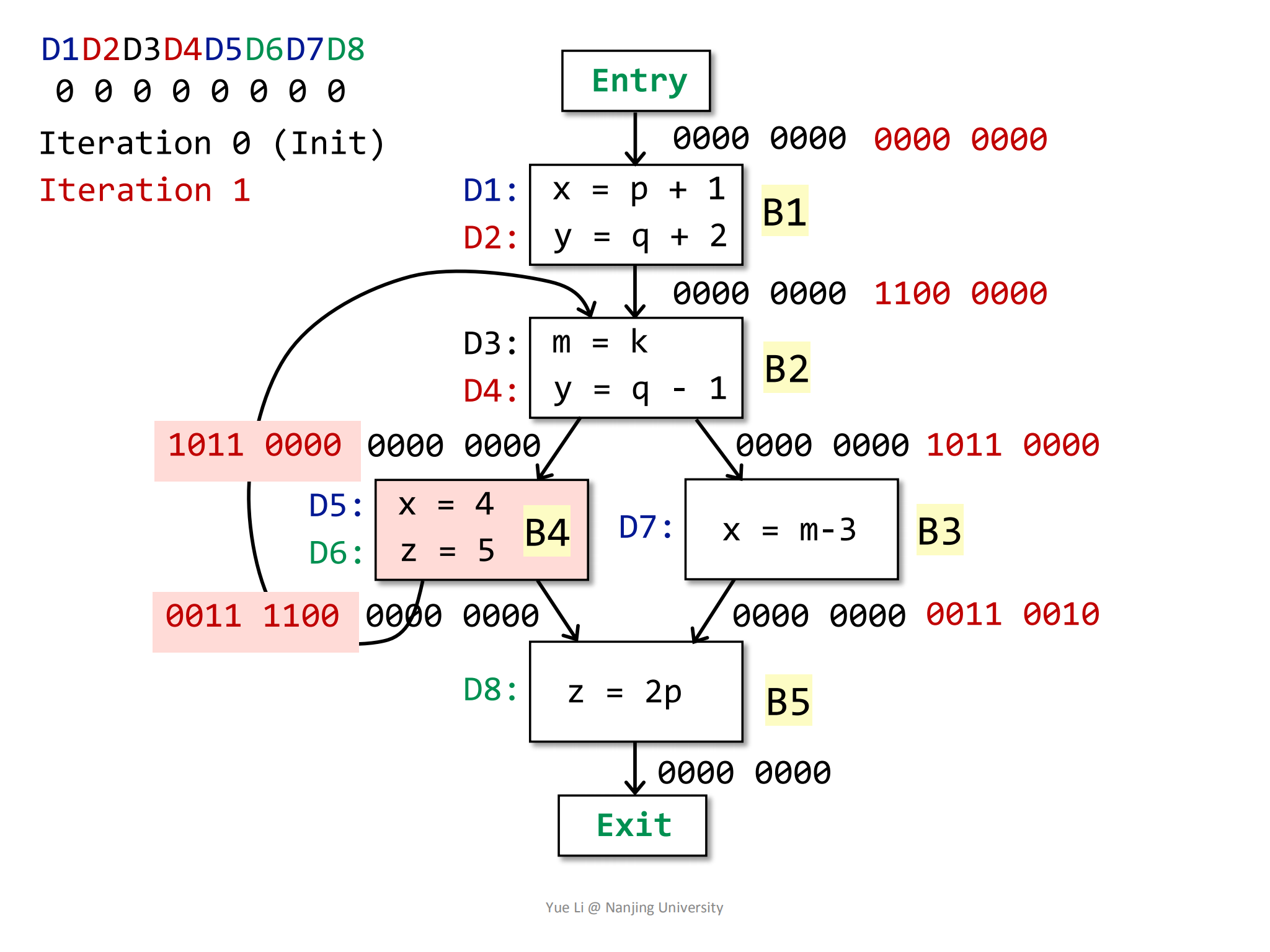

    28

  5. 最后计算B5的IN和OUT：

    1
    2
    3
    IN[B5] = OUT[B3] U OUT[B4]
    	   = 0011 1100 U 0011 0010
    	   = 0011 1110

    OUT[B5]：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B5] = { D8 } = 0000 0001
    IN[B5] = 0011 1110
    kill[B5] = { D6 } = 0000 0100

    OUT[B5] = gen[B5] U (IN[B5] - kill[B5])
    		= 0000 0001 U (0011 1110 - 0000 0100)
    		= 0000 0001 U 0011 1010
    		= 0011 1011

    其中红色加粗框中的0011 1110表示IN[B5]：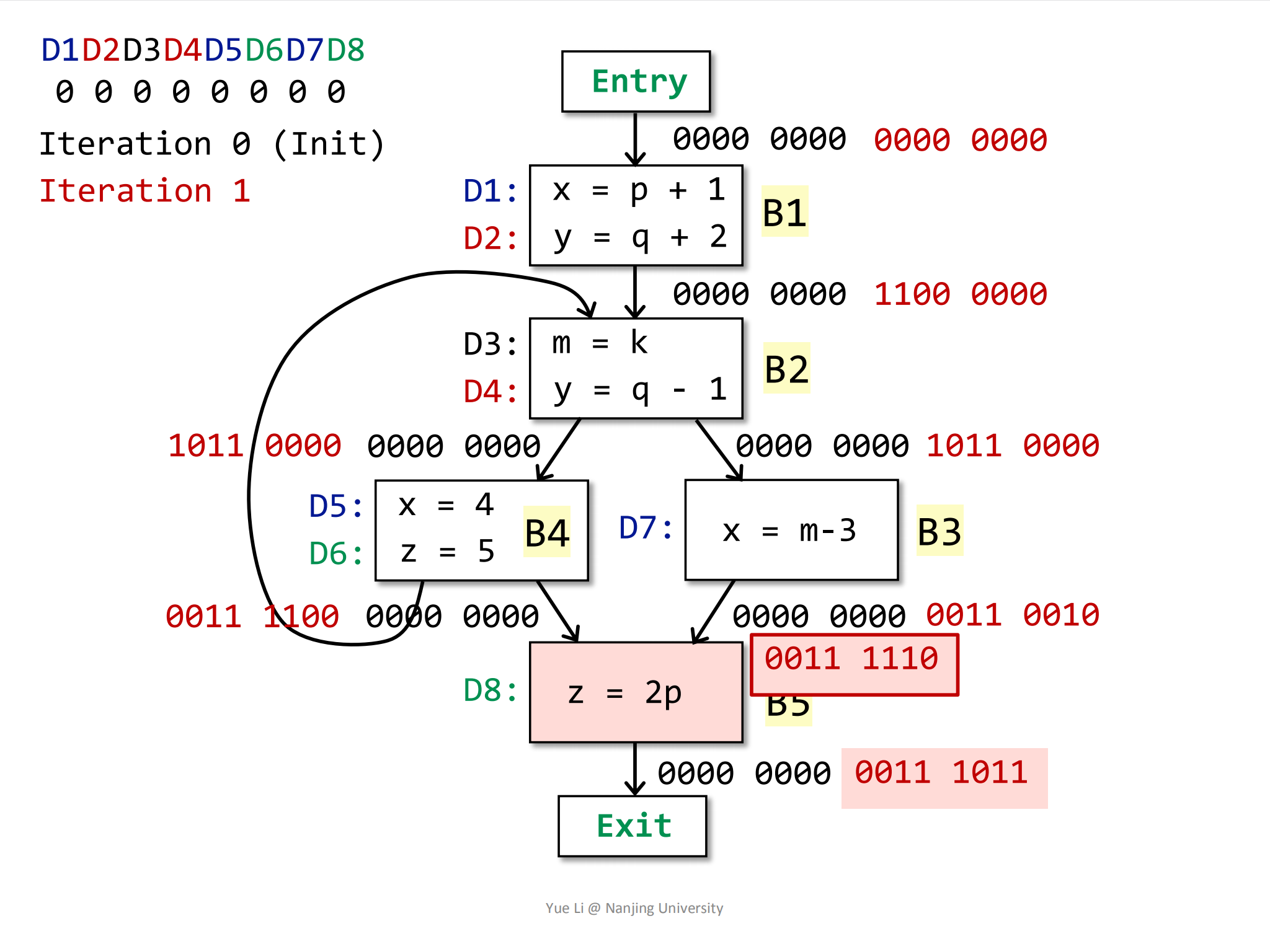

    29

到这里为止，第一遍遍历就结束了。在第一遍遍历结束之后，根据算法，要不要继续进行遍历取决于是否有OUT[B]发生变化，从上图的结果很容易可以看过，OUT[B1]，OUT[B2]，OUT[B3]，OUT[B4]和OUT[B5]全部都发生了变化，所以遍历继续进行。

第二轮迭代

  1. 第二轮迭代还是从B1块开始，首先是IN，还是从entry block进来，所以不会发生变化：

    1
    2
    IN[B1] = IN[entry]
    	   = 0000 0000

    然后是OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B1] = { D1, D2 } = 1100 0000
    IN[B1] = 0000 0000
    kill[B1] = { D4, D5, D7 } = 0001 1010

    OUT[B1] = gen[B1] U (IN[B1] - kill[B1])
    	    = 1100 0000 U (0000 0000 - 0001 1010)
    	    = 1100 0000 U 0000 0000
    	    = 1100 0000

    相较上一次的结果，OUT[B1]没有发生变化。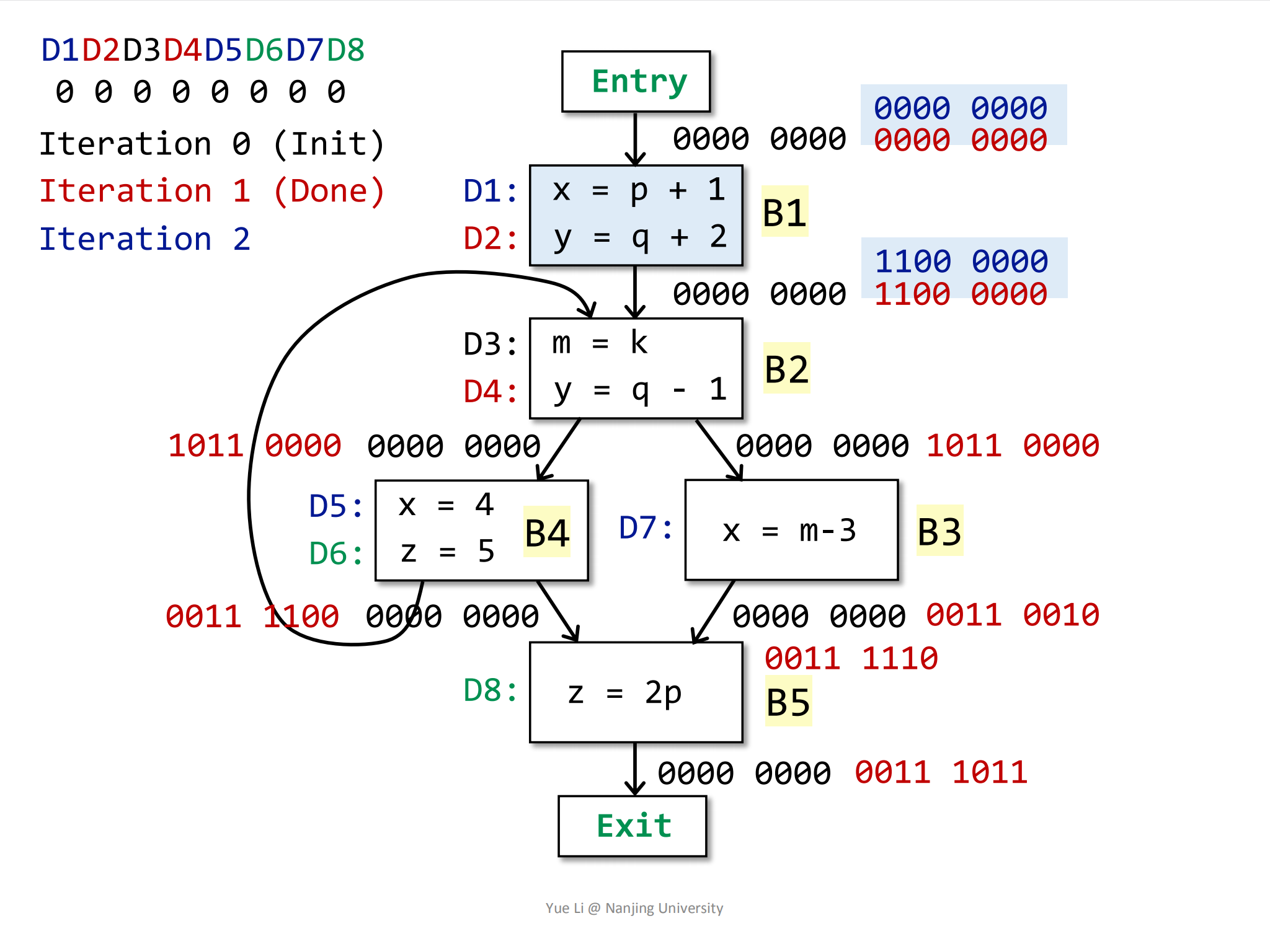

    30

  2. 接着看B2：

    1
    2
    3
    IN[B2] = OUT[B1] U OUT[B4]
    	   = 1100 0000 U 0011 1100
    	   = 1111 1100

    B2块的OUT为：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B2] = { D3, D4 } = 0011 0000
    IN[B2] = 1111 1100
    kill[B2] = { D2 } = 0100 0000

    OUT[B2] = gen[B2] U (IN[B2] - kill[B2])
    		= 0011 0000 U (1111 1100 - 0100 0000)
    		= 0011 0000 U 1011 1100
    		= 1011 1100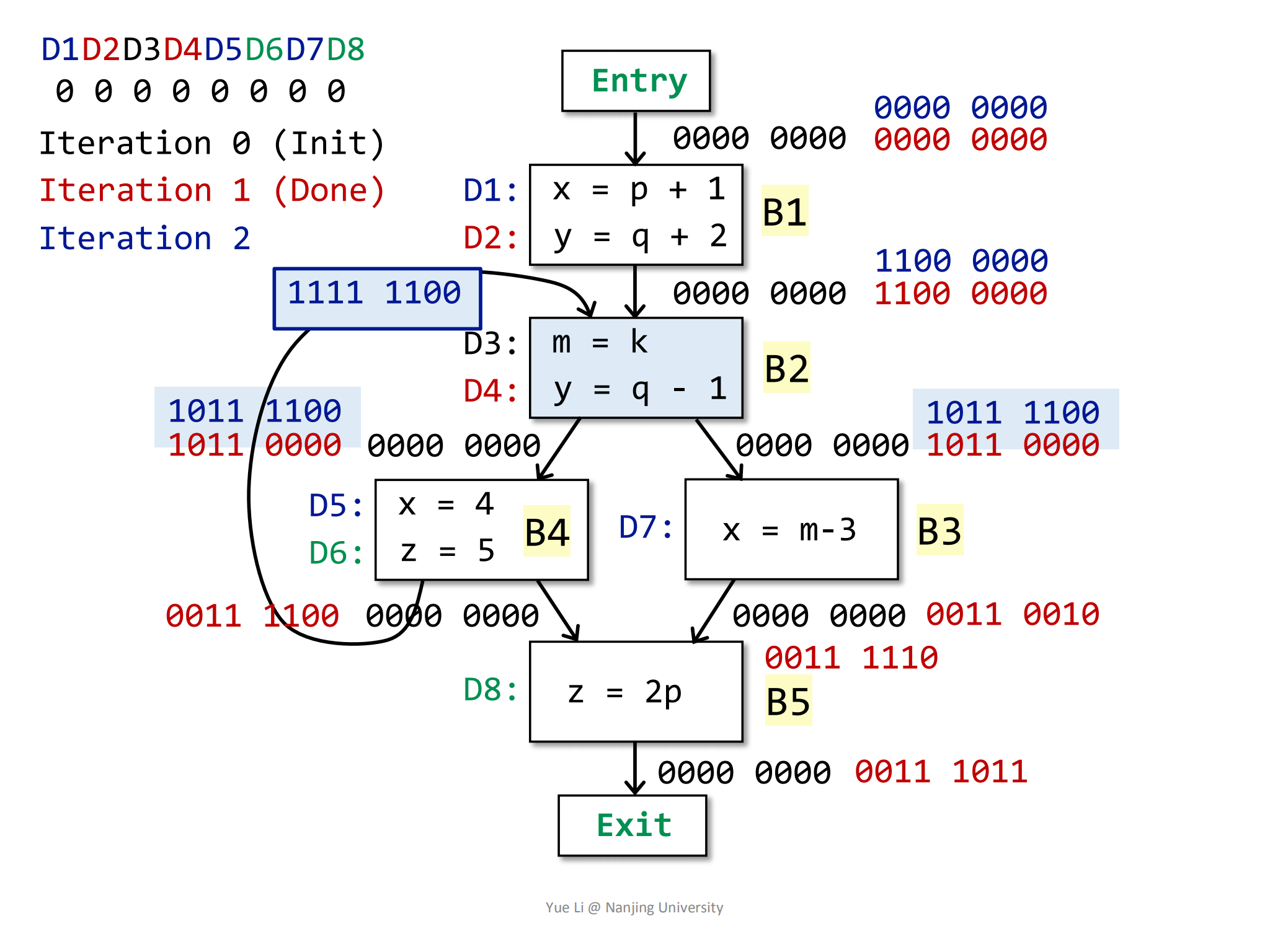

    31

    蓝色加粗方框里的是OUT[B1]+OUT[B4]的结果，最后得到的OUT[B2]是1011 1100，相较于前一轮的结果，发生了变化。

  3. 接着是B3块：

    1
    IN[B3] = OUT[B2] = 1011 1100

    然后是OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B3] = { D7 } = 0000 0010
    IN[B3] = 1011 1100
    kill[B3] = { D1, D5 } = 1000 1000

    OUT[B3] = gen[B3] U (IN[B3] - kill[B3])
    		= 0000 0010 U (1011 1100 - 1000 1000)
    		= 0000 0010 U 0011 0100
    		= 0011 0110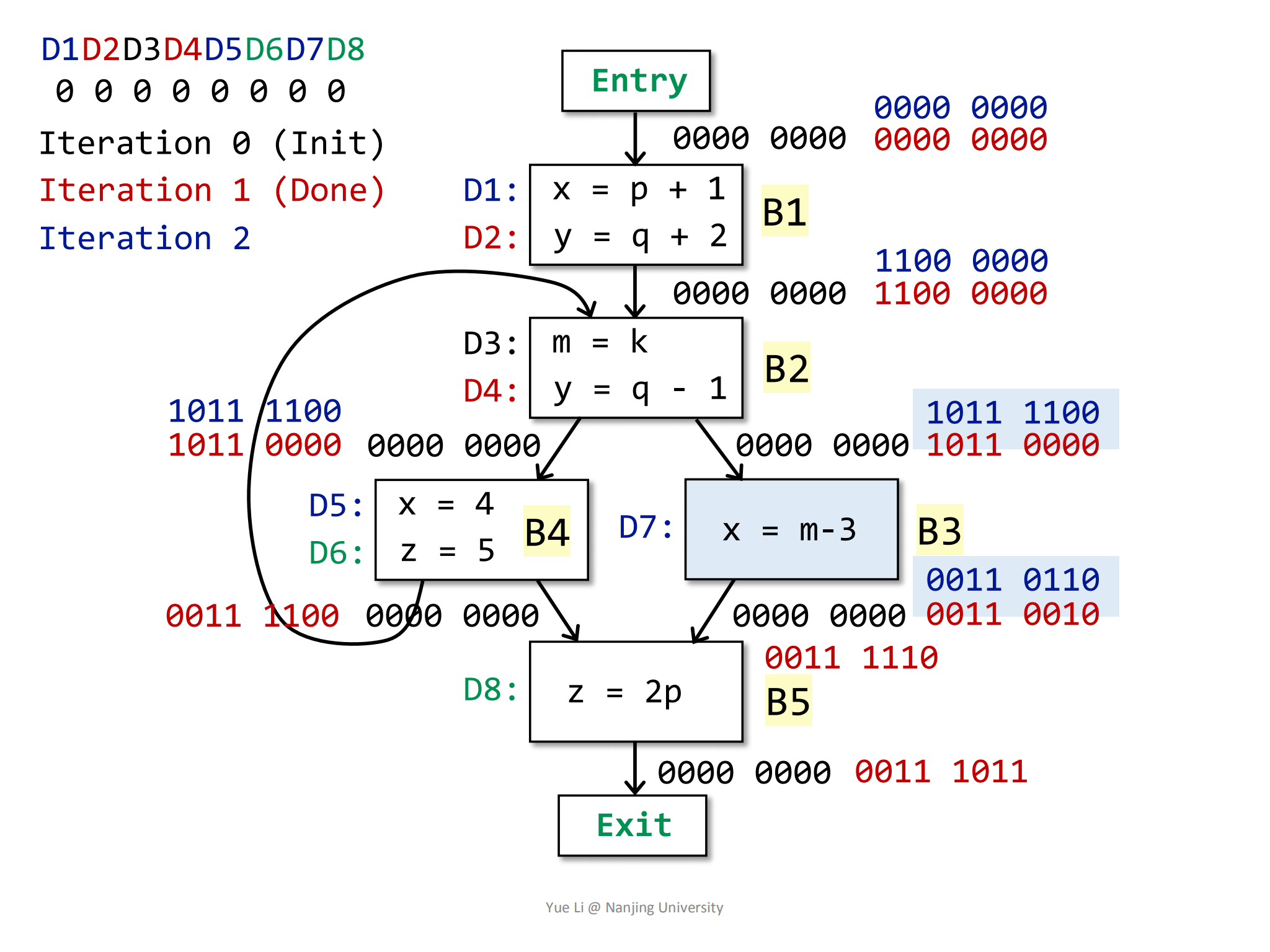

    32

    相较于上一轮的结果，OUT[B3]也发生了改变。

  4. 然后是计算B4块的IN和OUT：

    1
    IN[B4] = IN[B2] = 1011 1100

    然后是OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B4] = { D5, D6 } = 0000 1100
    IN[B4] = 1011 1100
    kill[B4] = { D1, D7, D8 } = 1000 0011

    OUT[B4] = gen[B4] U (IN[B4] - kill[B4])
    		= 0000 1100 U (1011 1100 - 1000 0011)
    		= 0000 1100 U 0011 1100
    		= 0011 1100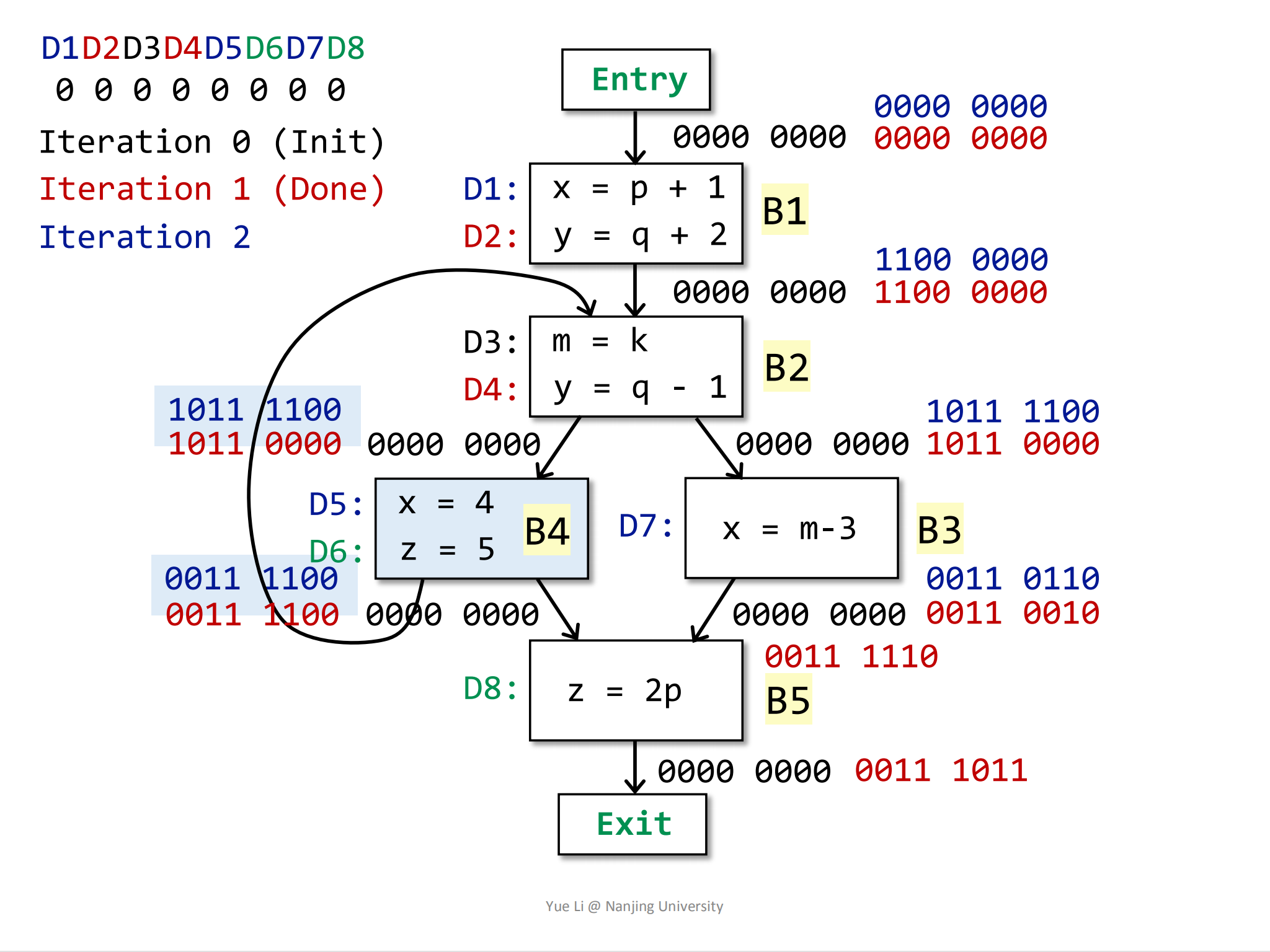

    33

    可以看到相比上一轮的结果，OUT[B4]也没有发生改变。

  5. 第二轮迭代的最后一个BB块，B5：

    1
    2
    3
    IN[B5] = OUT[B3] U OUT[B4]
    	   = 0011 0110 U 0011 1100
    	   = 0011 1110

    然后计算OUT[B5]：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B5] = { D8 } = 0000 0001
    IN[B5] = 0011 1110
    kill[B5] = { D6 } = 0000 0100

    OUT[B5] = gen[B5] U (IN[B5] - kill[B5])
    		= 0000 0001 U (0011 1110 - 0000 0100)
    		= 0000 0001 U 0011 1010
    		= 0011 1011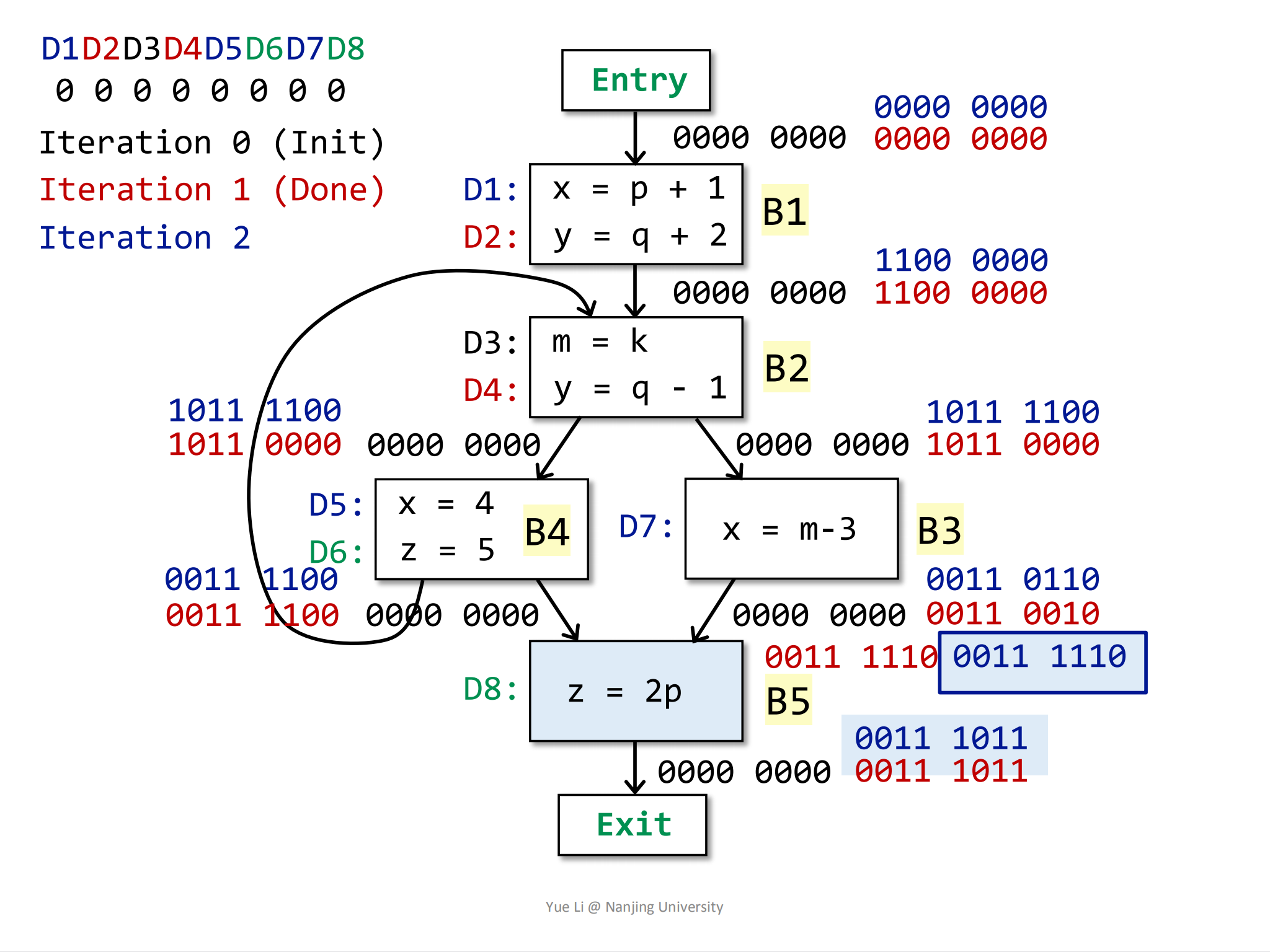

    34

    其中蓝色加粗框中表示的是IN[B5]，相比上一次的结果，OUT[B5]并没有发生改变。

执行到这一步，第二轮迭代也结束了。相比第一轮的迭代结果，OUT[B2]和OUT[B3]发生了改变。

第三轮迭代

因为OUT[B2]和OUT[B3]发生了变化，所以迭代继续。

  1. 从B1块开始，IN：

    1
    2
    IN[B1] = OUT[entry]
    	   = 0000 0000

    然后是OUT[B1]，其实因为我们知道IN[B1]没有发生改变，而且gen[B1]和kill[B1]是不会发生改变的，因为这两个是由BB块，更准确地说是由BB块中的statement决定的，statement是不会发生改变的，所以gen[B1]和kill[B1]也是不会发生改变的，因此OUT[B1]也同样不会改变：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B1] = { D1, D2 } = 1100 0000
    IN[B1] = 0000 0000
    kill[B1] = { D4, D5, D7 } = 0001 1010

    OUT[B1] = gen[B1] U (IN[B1] - kill[B1])
    	    = 1100 0000 U (0000 0000 - 0001 1010)
    	    = 1100 0000 U 0000 0000
    	    = 1100 0000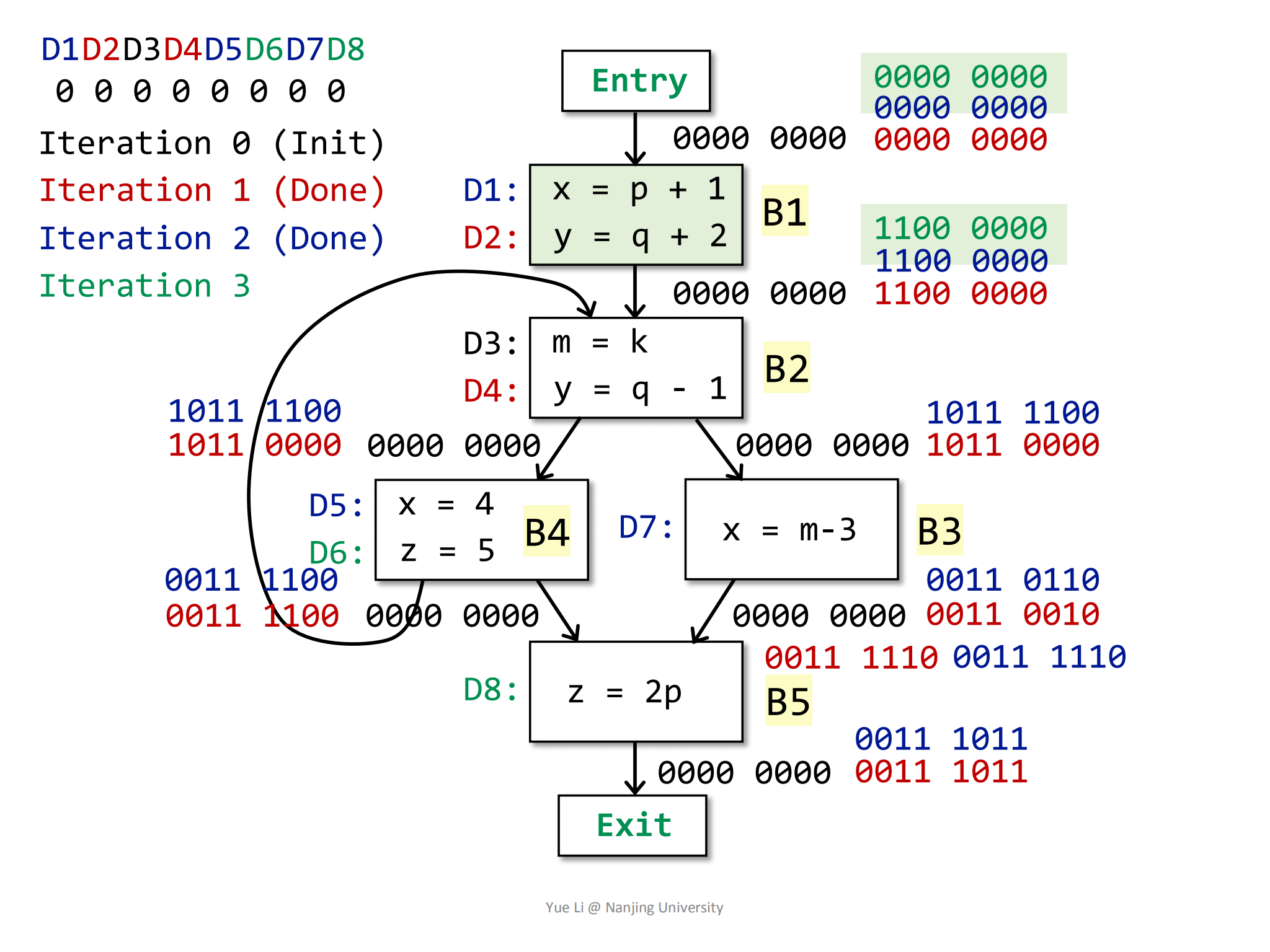

    35

  2. 然后是计算B2，首先是IN[B2]：

    1
    2
    3
    IN[B2] = OUT[B1] U OUT[B4]
    	   = 1100 0000 U 1011 1100
    	   = 1111 1100

    然后是OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B2] = { D3, D4 } = 0011 0000
    IN[B2] = 1111 1100
    kill[B2] = { D2 } = 0100 0000

    OUT[B2] = gen[B2] U (IN[B2] - kill[B2])
    		= 0011 0000 U (1111 1100 - 0100 0000)
    		= 0011 0000 U 1011 1100
    		= 1011 1100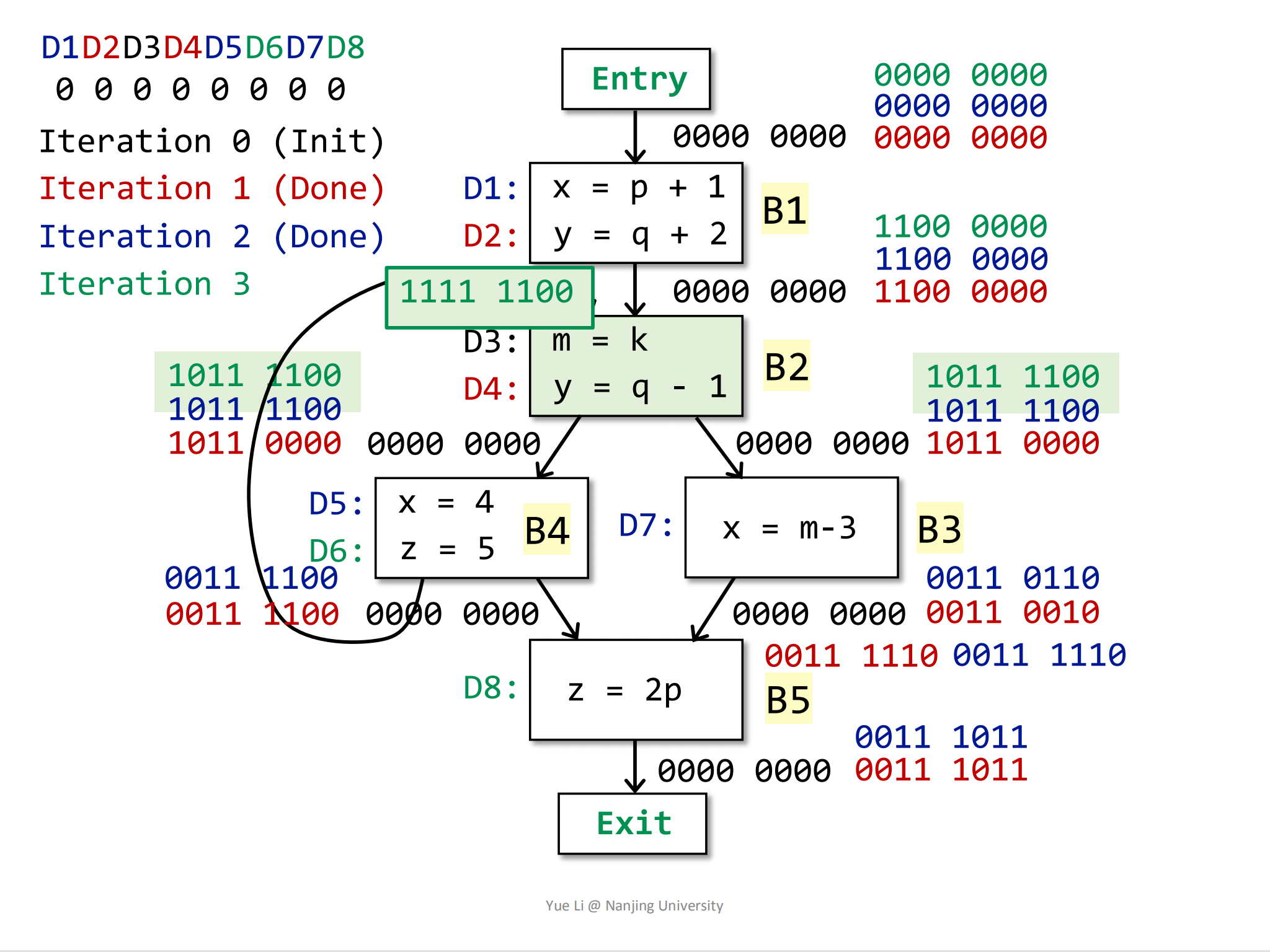

    36

    相较于第二轮迭代，OUT[B2]没有发生变化。加粗绿框中的是IN[B2]。

  3. 接着是B3，我们已经知道，因为OUT[B2]没有发生变化，所以B3块的IN和OUT也不会发生任何变化：

    1
    2
    IN[B3] = OUT[B2]
    	   = 1011 1100

    然后是OUT[B3]：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B3] = { D7 } = 0000 0010
    IN[B3] = 1011 1100
    kill[B3] = { D1, D5 } = 1000 1000

    OUT[B3] = gen[B3] U (IN[B3] - kill[B3])
    		= 0000 0010 U (1011 1100 - 1000 1000)
    		= 0000 0010 U 0011 0100
    		= 0011 0110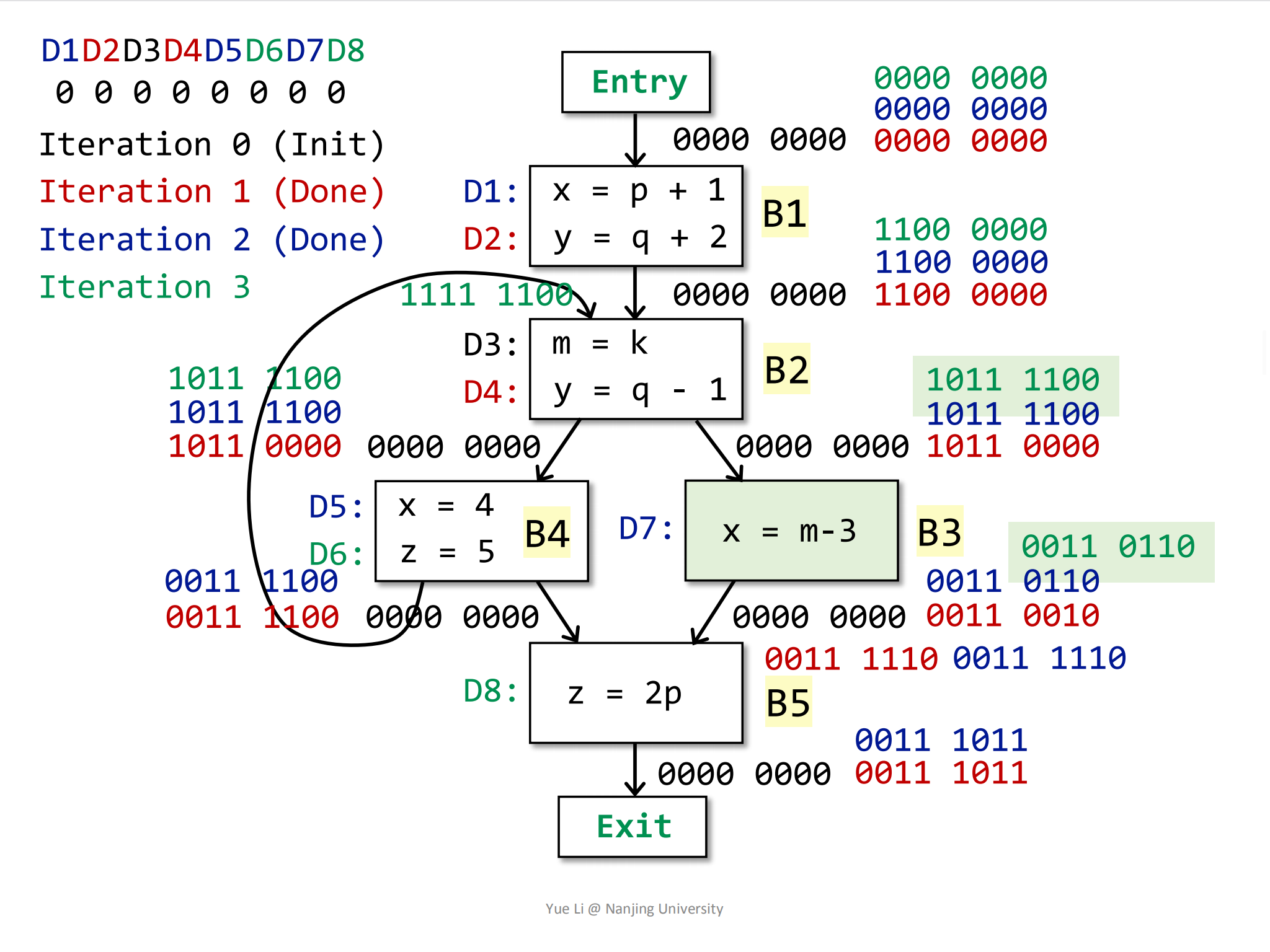

    37

  4. 然后是B4块，同样的，因为OUT[B2]没有发生改变，所以IN[B4]保持不变，顾OUT[B4]也不会发生变化：

    1
    IN[B4] = IN[B2] = 1011 1100

    计算OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B4] = { D5, D6 } = 0000 1100
    IN[B4] = 1011 1100
    kill[B4] = { D1, D7, D8 } = 1000 0011

    OUT[B4] = gen[B4] U (IN[B4] - kill[B4])
    		= 0000 1100 U (1011 1100 - 1000 0011)
    		= 0000 1100 U 0011 1100
    		= 0011 1100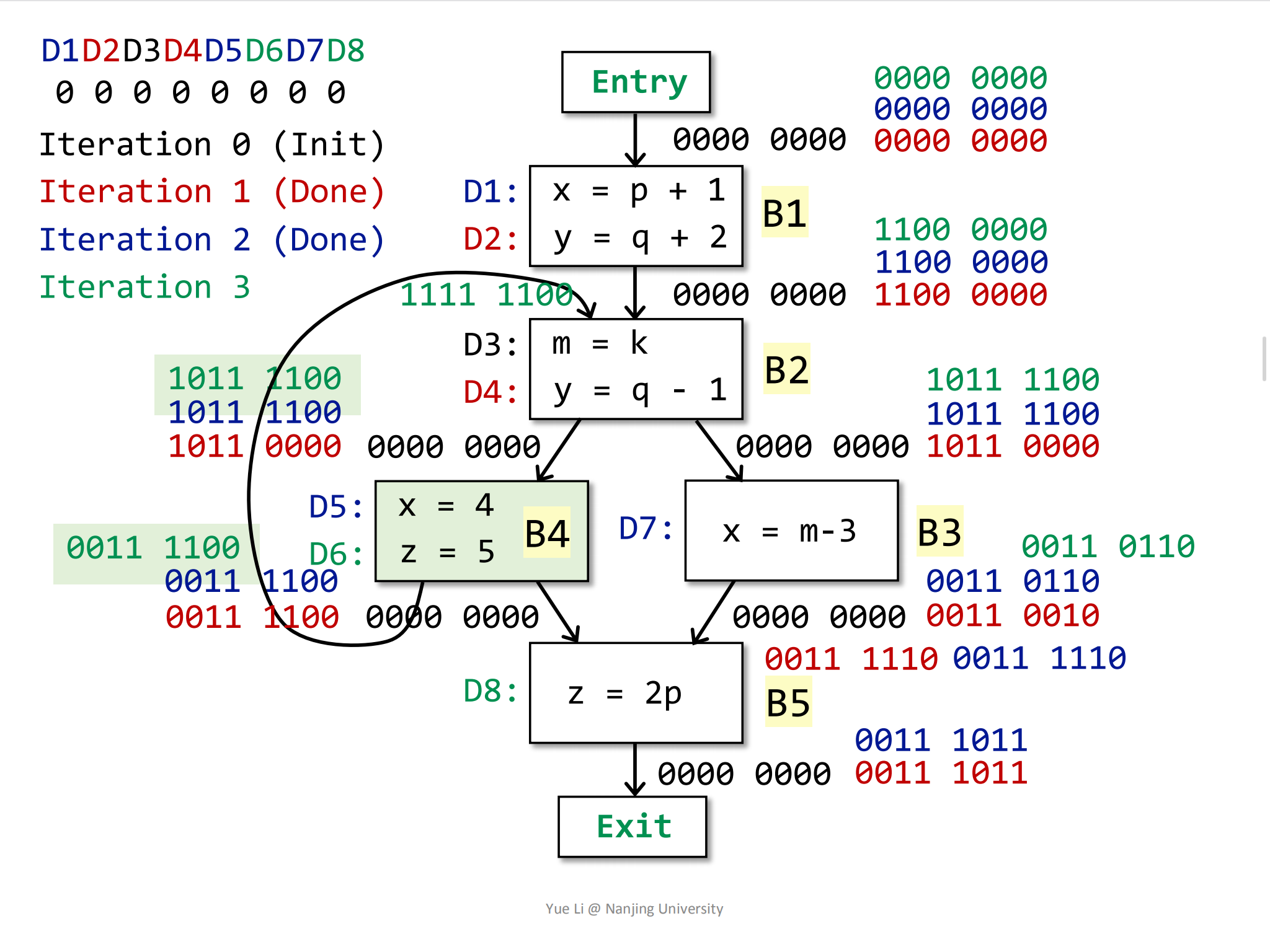

    38

  5. 最后是B5块，同样因为OUT[B4]和OUT[B3]保持不变，所以可以推出IN[B5]不变，那么OUT[B5]也不会发生变化

    1
    2
    3
    IN[B2] = OUT[B1] U OUT[B4]
    	   = 1100 0000 U 1011 1100
    	   = 1111 1100

    然后是OUT：

    1
    2
    3
    4
    5
    6
    7
    8
    gen[B2] = { D3, D4 } = 0011 0000
    IN[B2] = 1111 1100
    kill[B2] = { D2 } = 0100 0000

    OUT[B2] = gen[B2] U (IN[B2] - kill[B2])
    		= 0011 0000 U (1111 1100 - 0100 0000)
    		= 0011 0000 U 1011 1100
    		= 1011 1100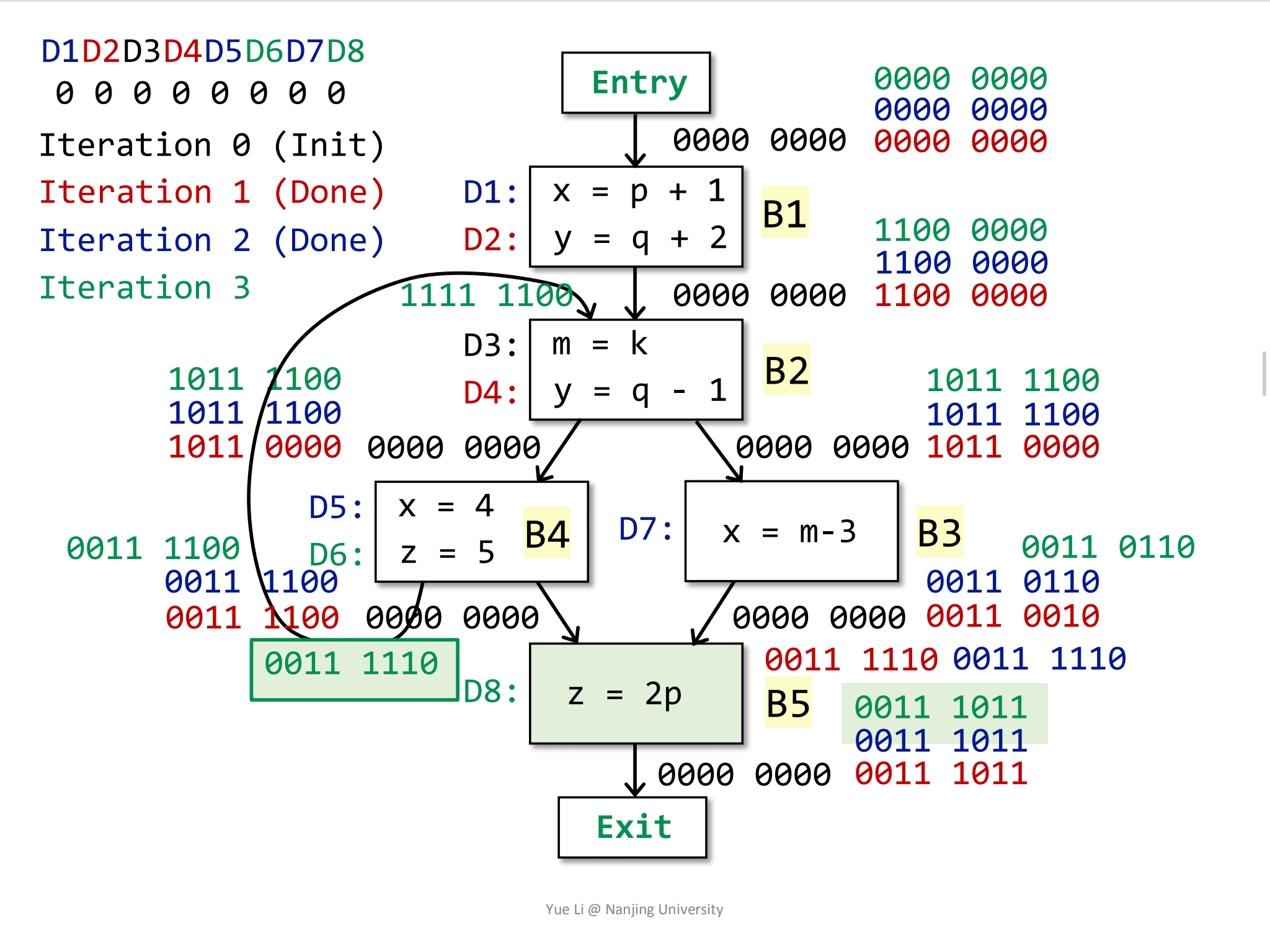

    39

第3轮遍历也正式结束，此时每个BasicBlock块的OUT都没有发生改变，所以迭代结束。

Reaching Definitions迭代原理

现在剩下一个问题需要我们思考：为什么迭代能够停下来？也就是说，为什么OUT[B]的变化会越来越少？

首先，gen[s]和kill[s]是不会发生改变的，因为这是statement本身决定的，而statement是不会改变的，故gen[s]和kill[s]不会发生改变。所以OUT[s]的变化其实是由IN[s]决定的。

40

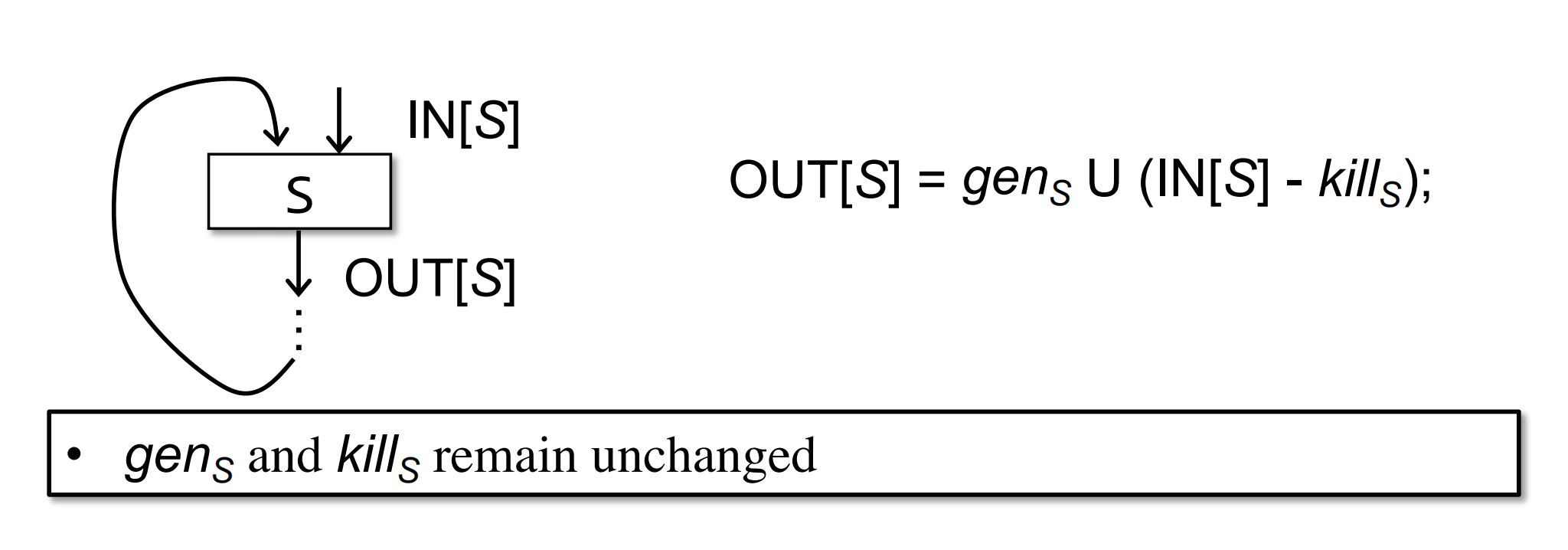
那么什么会导致IN[s]发生变化呢，IN[s]的变化其实是由more facts导致的，但是这个more facts对OUT的改变来说，只可能比之前更多，不可能比之前更少，因为他们要么是被kill[s]给kill掉，要么是保留下来称为survivor，所以OUT只会越来越多（简单点讲就是OUT中的1只会越来越多）。

41

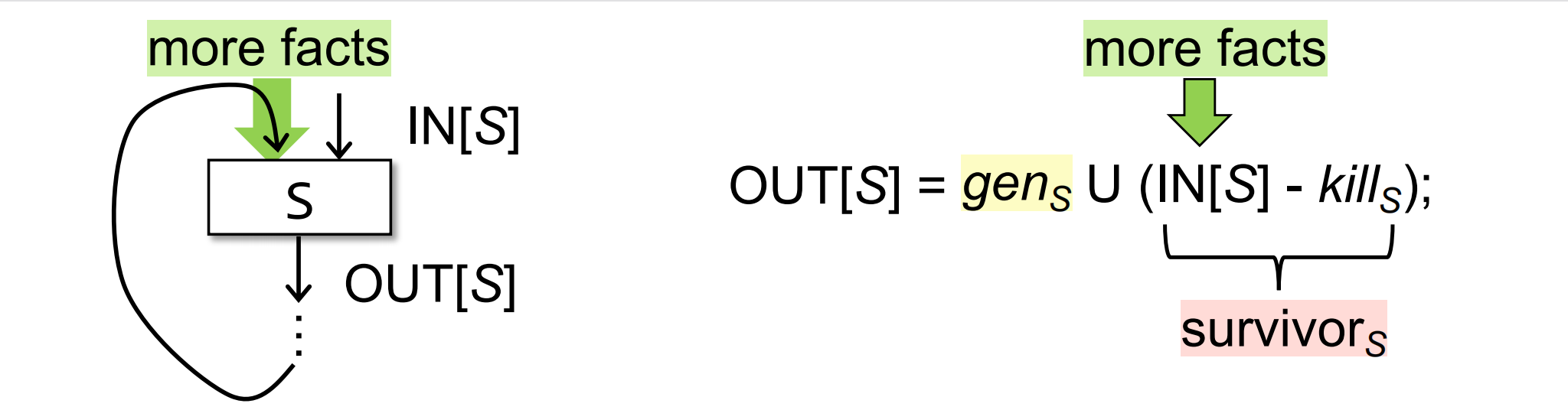
OUT中bit位的变化只有三种可能性：

  • 0 -> 0
  • 0 -> 1
  • 1 -> 1

不可能出现1->0，也就说不可能出现之前是1的definition突然被kill掉。

因为factsd是有限的，所以在不断加入facts的过程中，OUT也会慢慢收敛，直到OUT不再发生变化。

42

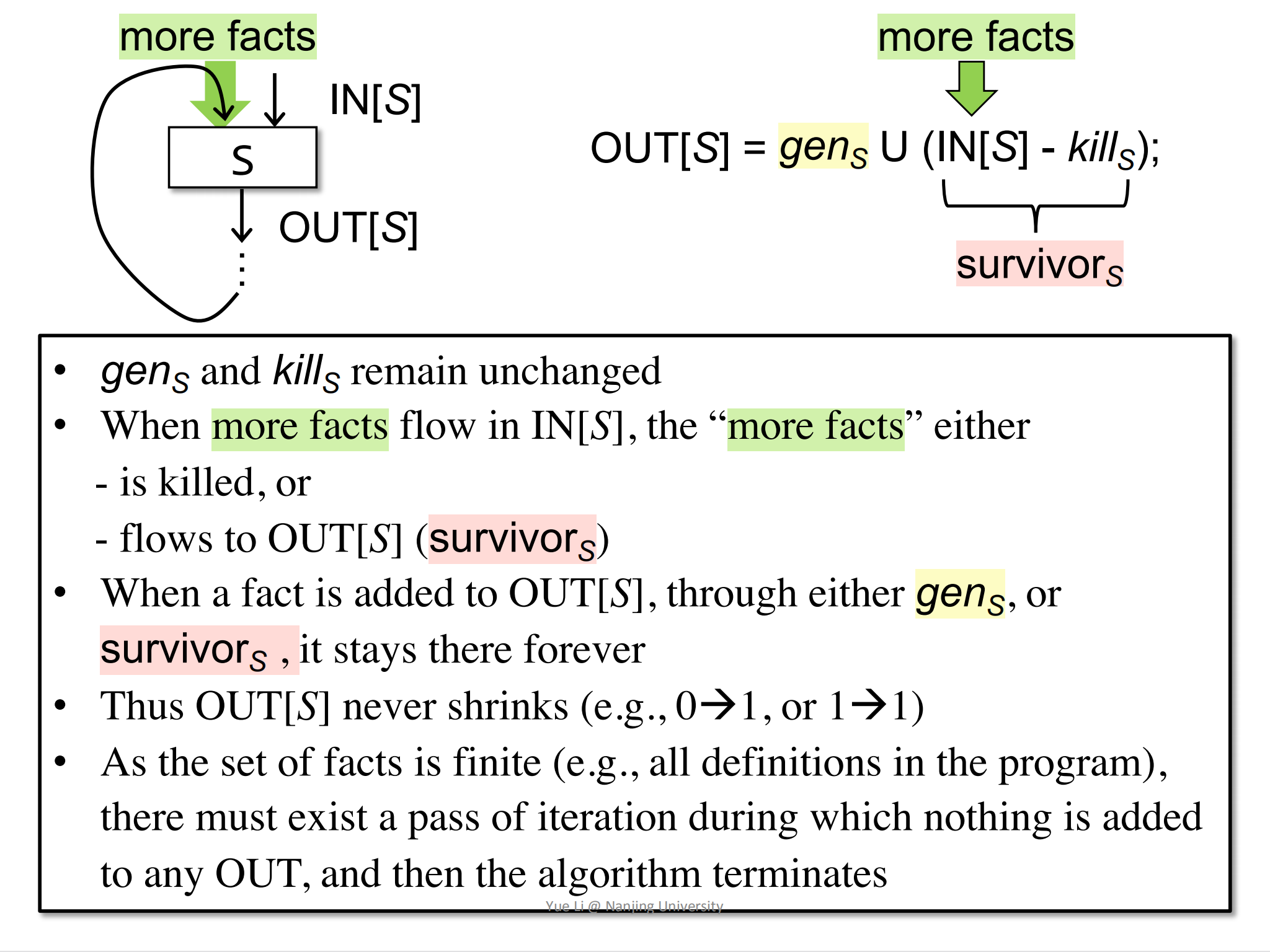
因为OUT不会再发生变化了，所以IN也不会发生变化了，而IN不会再变化的效果又作用在OUT上，从而达到一个平衡的状态，也就说程序达到了一个不动点（fix point），所以迭代的结束是以OUT不再改变作为标准。

43

小结

在Joern中DDG图的生成中，之前一直看不懂，学了这一小节课后，明白了类DDGCreator也是通过reaching definition迭代算法来讲CFG转化为DDG的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public class DDGCreator
{
	private boolean updateOut(Object x)
	{
		HashSet<Object> listForKey = out.getListForKey(x);
		HashSet<Object> oldOut = new HashSet<Object>(listForKey);

		out.removeAllForKey(x);

        /**
        * 根据OUT[x] = gen[x] U (IN[x] - kill[x])
       	* 先将IN[x]加入
        */
		// in(x)
		HashSet<Object> inForX = in.getListForKey(x);
		if (inForX != null)
		{
			for (Object o : inForX)
			{
				out.add(x, o);
			}
		}
        
		// 然后去掉kill[x]
		// -kill(x)
		List<Object> killX = cfg.getSymbolsDefined().get(x);
		if (killX != null)
		{

			Iterator<Object> it = out.getListForKey(x).iterator();
			while (it.hasNext())
			{
				Definition def = (Definition) it.next();
				if (killX.contains(def.identifier))
					it.remove();
			}

		}

       	// 再将gen(x)加入到out(x)集合中
		// gen(X)
		HashSet<Object> genX = gen.getListForKey(x);

		if (genX != null)
		{
			for (Object o : genX)
			{
				out.add(x, o);
			}
		}

		return !oldOut.equals(out.getListForKey(x));
	}
}