前言
上一节课学习了可达定义分析,这一节课开始学习Live Variables Analysis。
Live Variables Analysis介绍
Live Variables Analysis的目的是分析一个变量v是否可以在程序点p开始的路径上被使用。如果可以,则说明变量v在程序点p是live的,反之,就说变量v在程序点p是dead的。同时,变量v在程序点p是live的还需要满足一个隐藏条件:变量v在被使用之前,是不应该被重定义的。

Live Variable信息可以用于寄存器分配(register allocations)。假设在某个程序点,寄存器已经全部被使用了,但是执行下一条语句又必须使用寄存器来存储下一个操作数,所以我们只能进行替换,我们就可以用将dead variable对应的寄存器清出来使用。
区分ReachingDefinitions
上一节课的Reaching Definitions,关注的重点是Definitions,是有100个definitions,但是对应的变量可能没有100个:

而这一小节,关注的是Variables,是有100个变量。同样将这些变量抽象成bit,用bit vector来表示他们的状态:

上一节课的Reaching Definitions定义可达性分析中,分析是顺着control flow的方向进行的,也就是进行的forward analysis前向分析。
但是对于Live Variable Analysis来说,backward analysis更加方便。
假设现在有这样的控制流,在P点,变量v被定义,然后经过了语句B(语句B是什么我们不知道),然后语句B后面跟着两个分支语句S1和S2,其中S1中有一个assignment赋值语句,变量v出现在赋值语句的右边,也就是变量v被使用了。
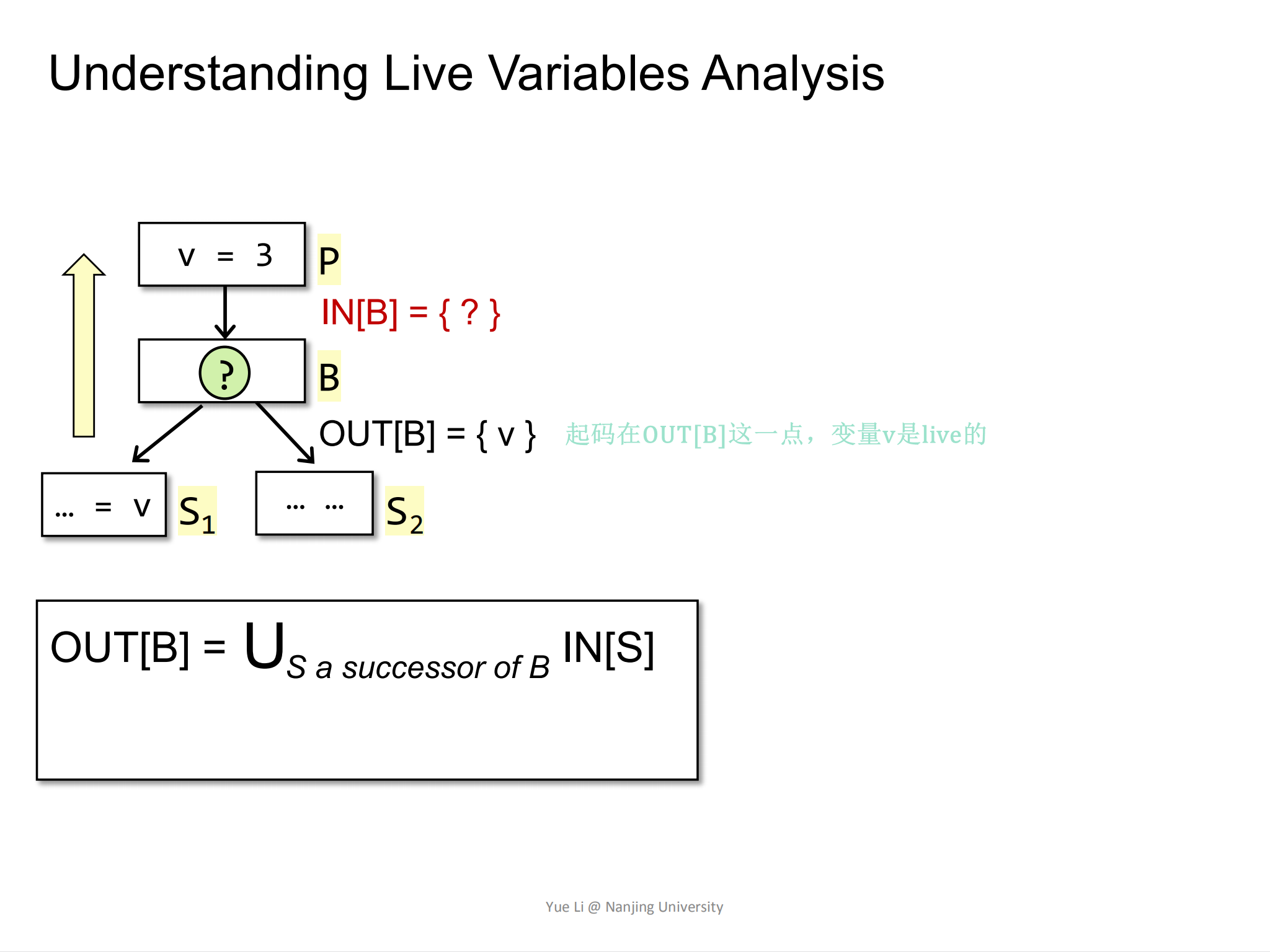
在上图中,语句B对应的OUT[B]经过对它的后继节点(S1和S2)求交集处理之后,发现OUT[B] = v,这说明了,至少在OUT[B]这一点,变量v是live的。
Live Variable Analysis是一种may analysis,因为我们不能放过任何一条可能使用了变量v的路径。因为这是一种may analysis,所以是对各个子集做一个Union(取并集)操作,如果是一个must analysis,就有可能对其进行一个取交集操作。当然,处理方式并不是仅仅只有取交集或是取并集这两种操作。
现在已经知道了OUT[B] = { v },所以我们接下来要求解IN[B]是什么。
先看看下面6个例子,分别假设BasicBlockB有下面6种情况,分别求解IN[B]是什么:

第一种情况:
1
k = n
变量v没有被重新定义,所以显然
IN[B] = { v }。第二种情况:
1
k = v
变量v没有被重新定义,只是在BasicBlock B这里被使用了,所以
IN[B] = { v }。第三种情况:
1
v = 2
变量v被重新定义了,所以在
IN[B]对应的程序点处,变量v就是dead状态的,所以IN[B] = { }。第四种情况:
1
v = v - 1
这种情况稍微复杂一点,在这一点,变量v先被使用了(v - 1),接着变量v被重新定义了,所以对于程序点
IN[B]时,变量v还是live状态的,因为它可以传递到BasicBlock B处先被使用,被使用时变量v还没有发生变化,被赋值后才发生了改变,所以IN[B] = { v }。第五种情况:
1
2v = 2
k = v这种情况其实和第四种情况是一样的,变量v是先被使用后被重新定义redefined,所以,程序点
IN[B]处的变量v还是live状态的,所以IN[B] = { v }。第六种状态:
1
2k = v
v = 2这种状态和前面两种状态是相反的。变量v先被重新定义了,然后才被使用,所以,对于程序点
IN[B],变量v已经是dead状态,所以这种状态下IN[B] = { }。
最后的结果为:

所以得到的control flow信息和transfer function为:
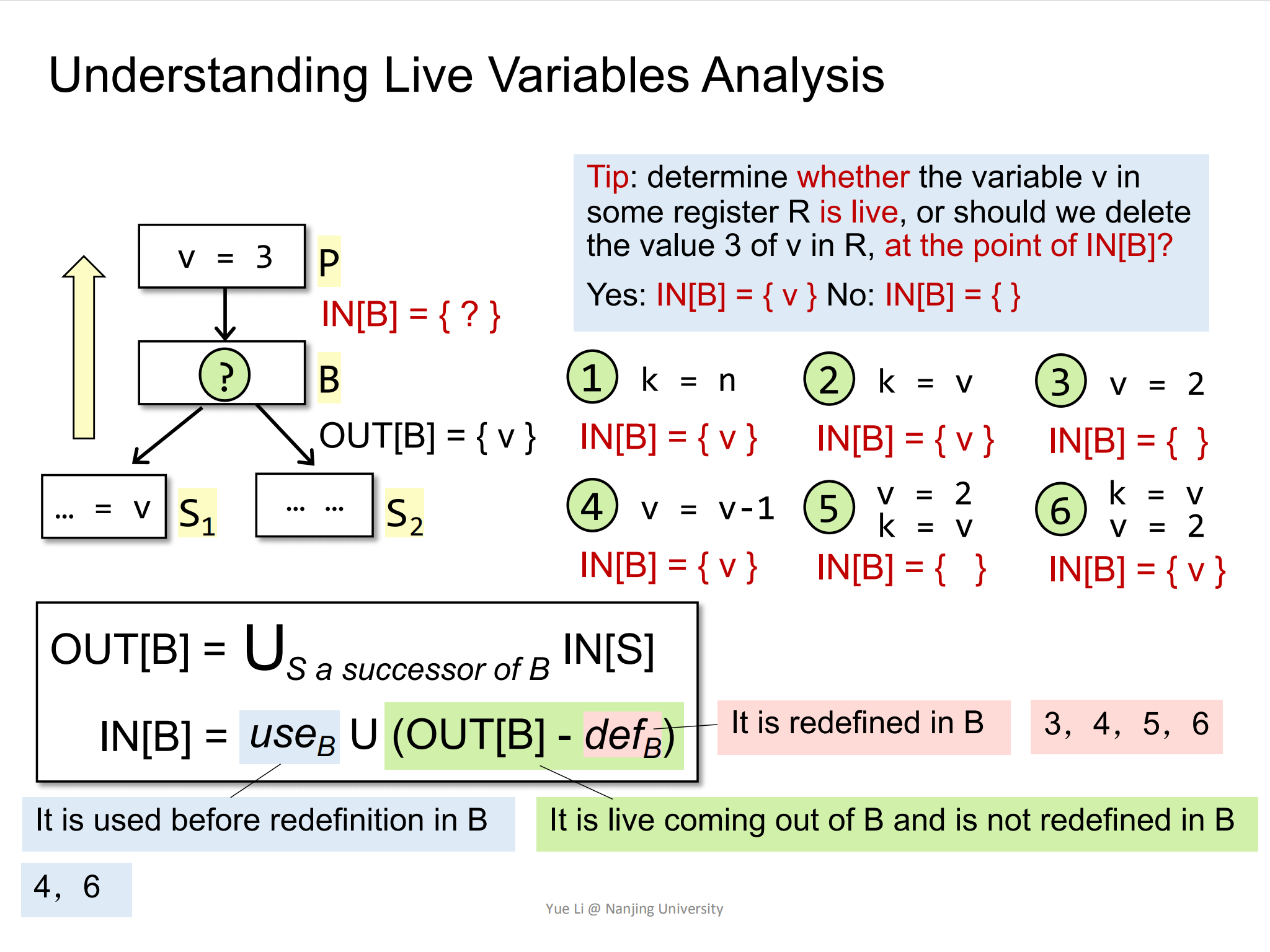
其中use[B]只有在变量的use发生在redefine之前才有效。
Live Variables迭代算法
Live Variables迭代算法和上一节课的Reaching Definitions迭代算法很像,如下图所示:

因为是backward analysis,是从OUT求解IN,所以boundary value(边界值)是IN[exit] = ∅。在一般情况下,may analysis的初始化是将其初始化为空集∅。
然后算法的主要处理部分是分别进行control flow处理求解OUT[B],然后再利用transfer function求解IN[B]。然后不停地迭代,直到没有IN发生变化。
Live Variables算法实例
现在有这样一段控制流,一共涉及7个变量(x,y,z,p,q,m,k),将其分为5个BasicBlock(B1,B2,B3,B4,B5):
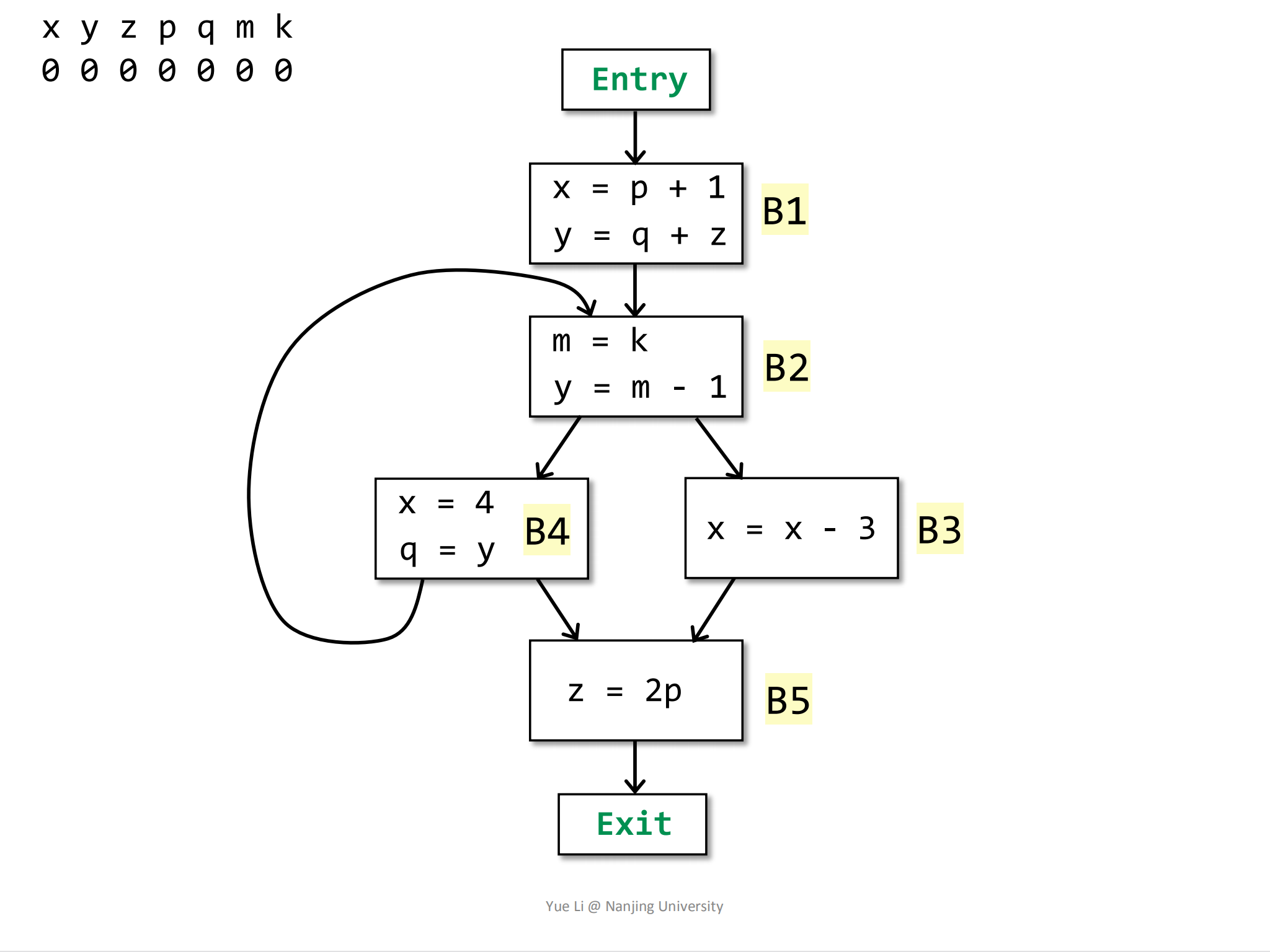
初始化
在正式开始迭代之前,先将所有的IN初始化为0000 000:
1 | IN[exit] = 000 0000 |
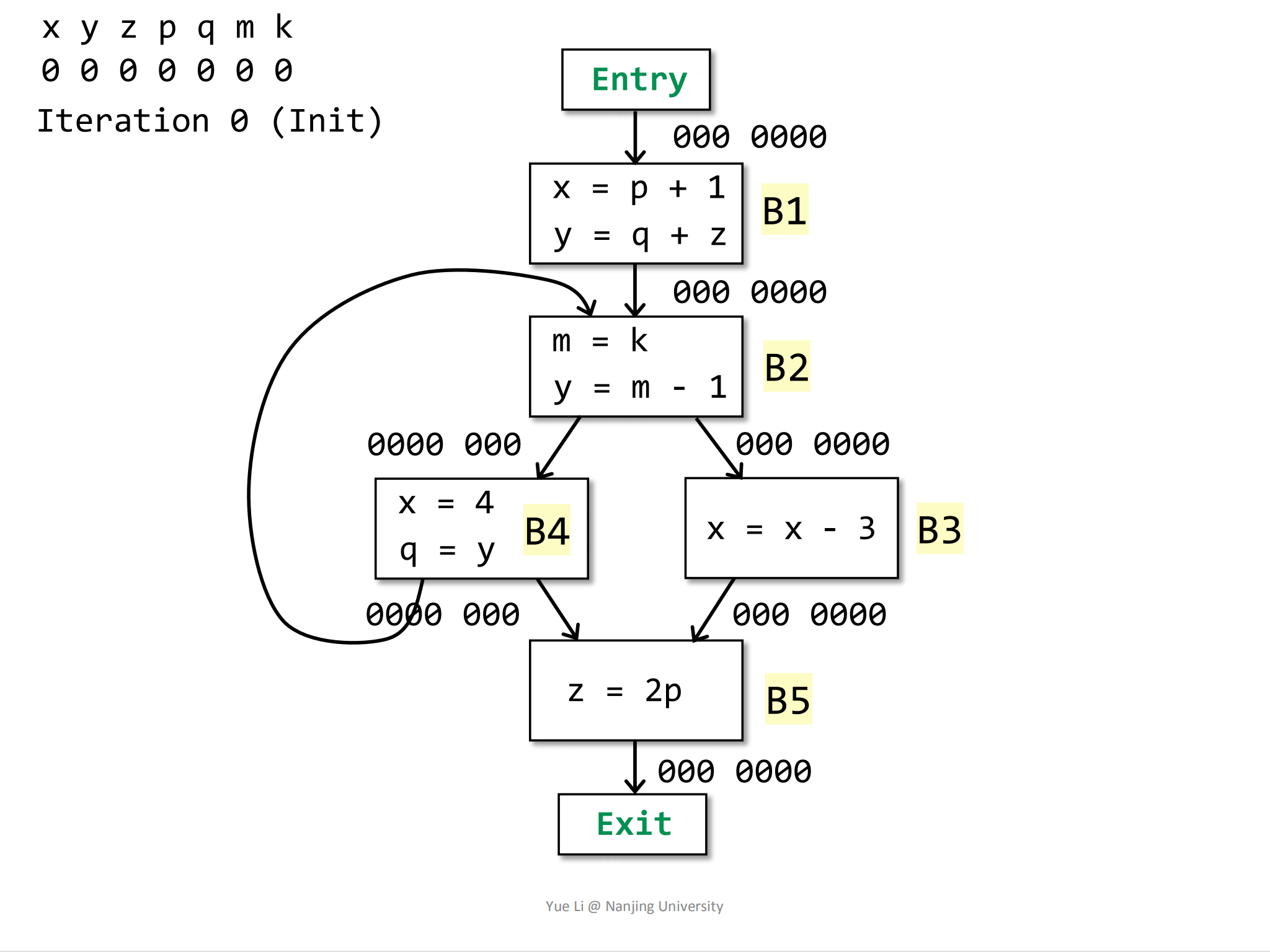
第一轮迭代
首先处理B5的control flow信息,得到
OUT[B5]:1
2OUT[B5] = IN[exit]
= 000 0000然后利用transfer function来计算
IN[B5]:1
2
3
4
5
6
7
8use[B5] = { p } = 000 1000
OUT[B5] = 000 0000
def[B5] = { z } = 001 0000
IN[B5] = use[B5] U (OUT[B5] - def[B5])
= 000 1000 U (000 0000 - 001 0000)
= 000 1000 U 000 0000
= 000 1000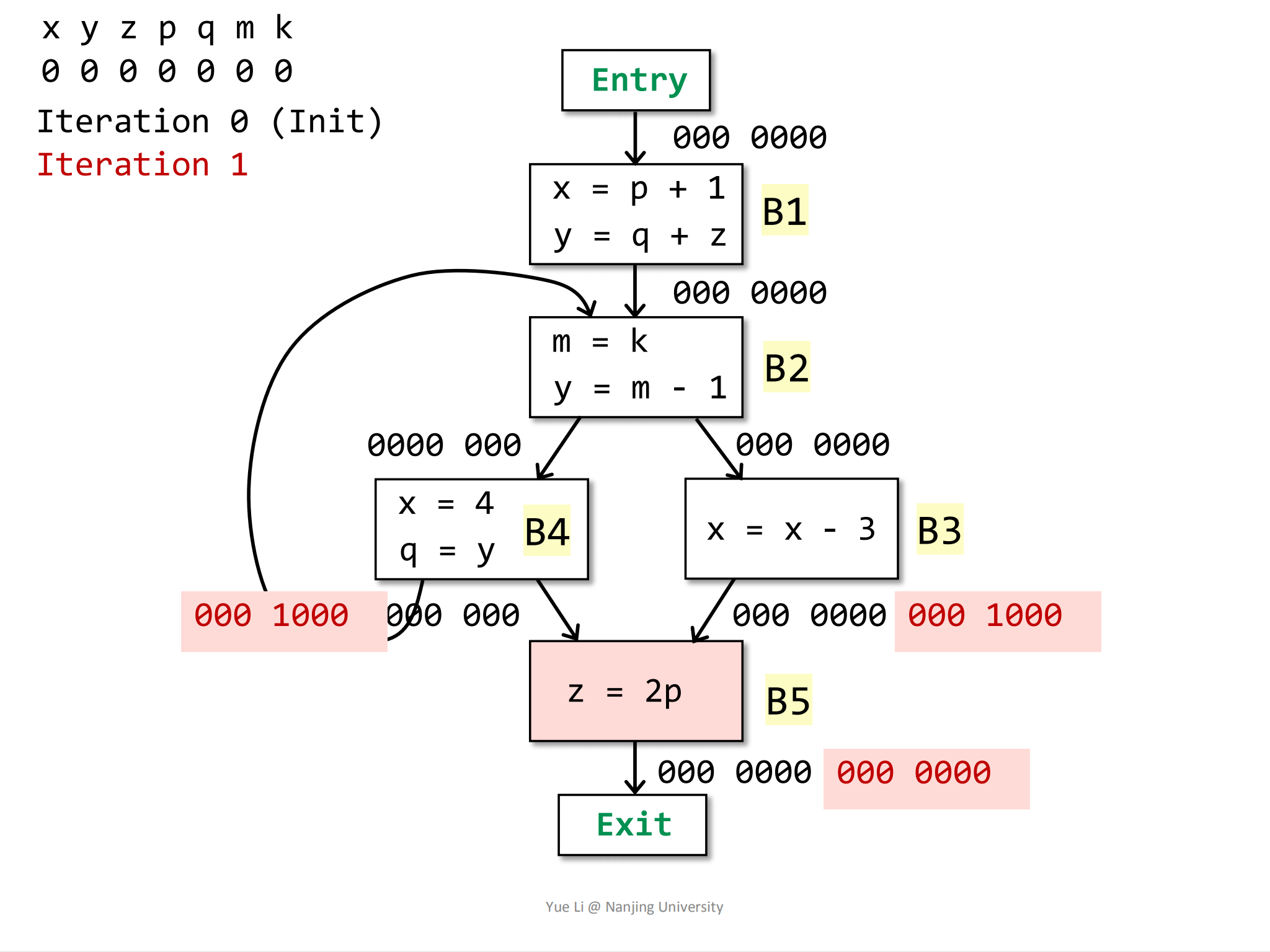
接着求解B3,根据控制流信息得到
OUT[B3]:1
2OUT[B3] = IN[B5]
= 000 1000然后根据转换函数求解
IN[B3],这里要注意x = x - 3,和之前的例子一样,变量x是先被使用,后被重新定义的,所以use[B3] = { x }:1
2
3
4
5
6
7
8use[B3] = { x } = 100 0000
OUT[B3] = 000 1000
def[B3] = { x } = 100 0000
IN[B3] = use[B3] U (OUT[B3] - def[B3])
= 100 0000 U (000 1000 - 100 0000)
= 100 0000 U 000 1000
= 100 1000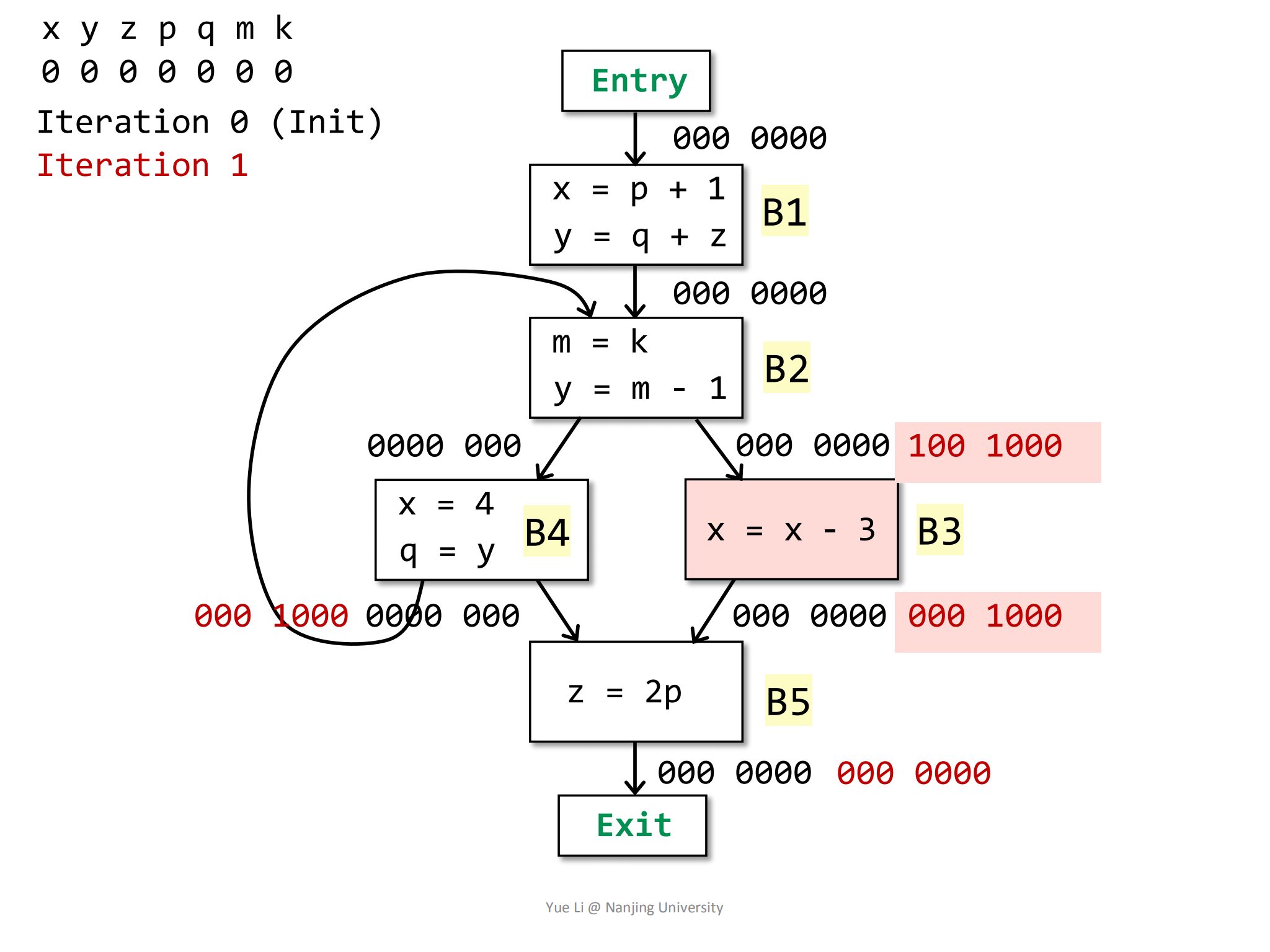
接着看B4块,根据控制流处理
OUT[B4],B4的后继节点为B2和B5:1
2
3OUT[B4] = IN[B2] U IN[B5]
= 000 0000 U 000 1000
= 000 1000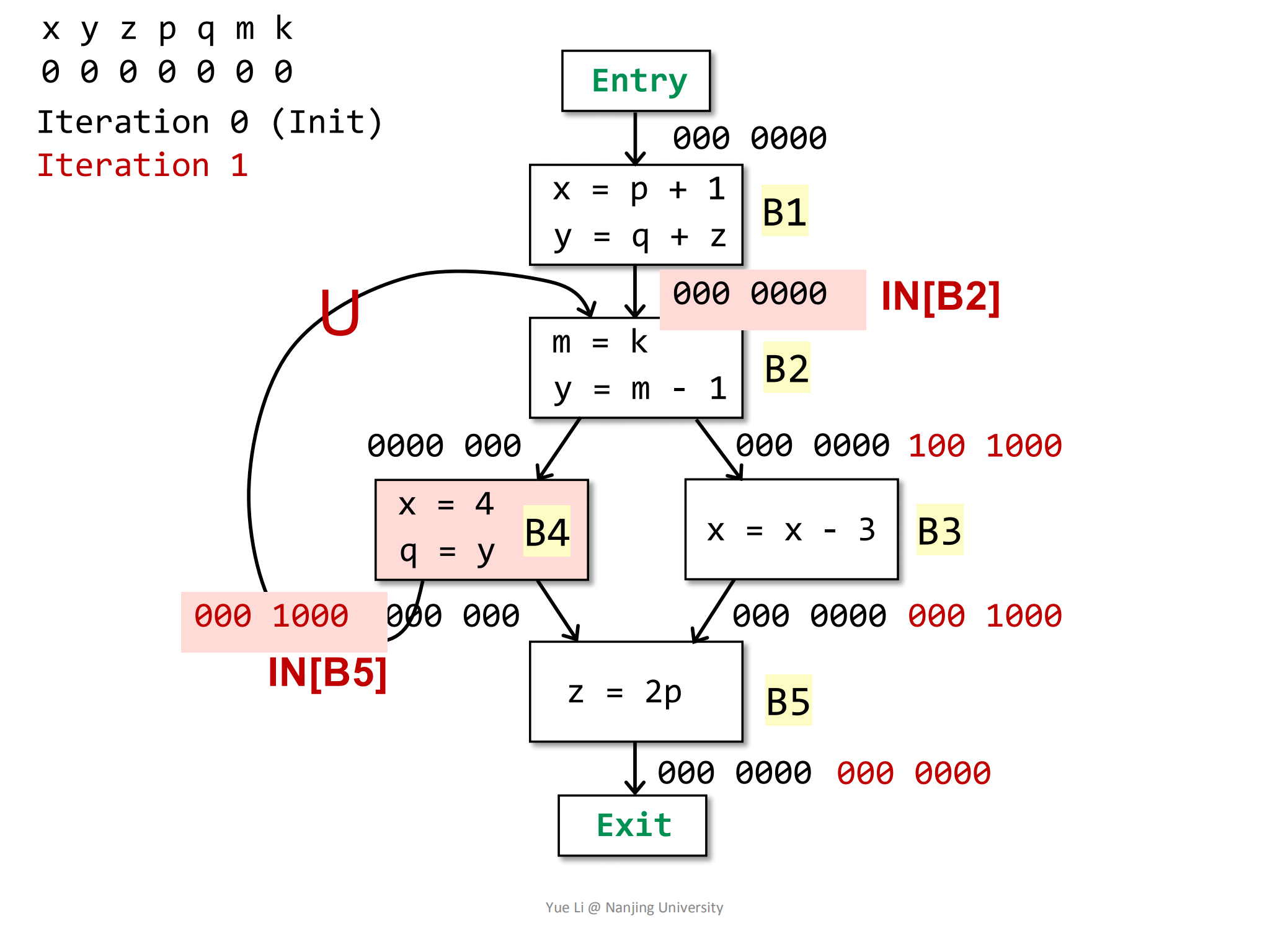
然后根据transfer function计算
IN[B4]:1
2
3
4
5
6
7
8use[B4] = { y } = 010 0000
OUT[B4] = 000 1000
def[B4] = { x, q } = 100 0100
IN[B4] = use[B4] U (OUT[B4] - def[B4])
= 010 0000 U (000 1000 - 100 0100)
= 010 0000 U 000 1000
= 010 1000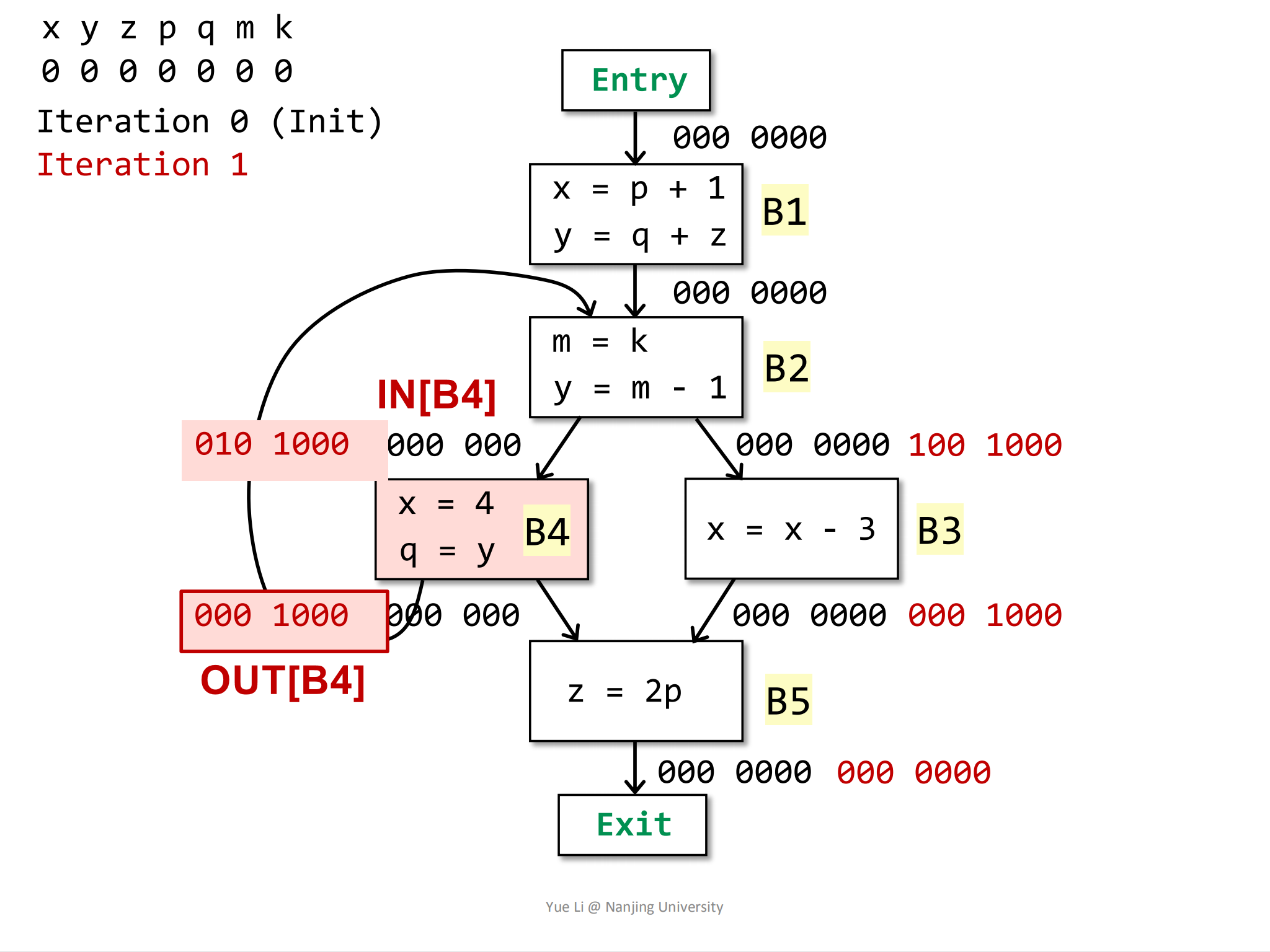
然后求解B2块的OUT信息:
1
2
3OUT[B2] = IN[B3] U IN[B4]
= 100 1000 U 010 1000
= 110 1000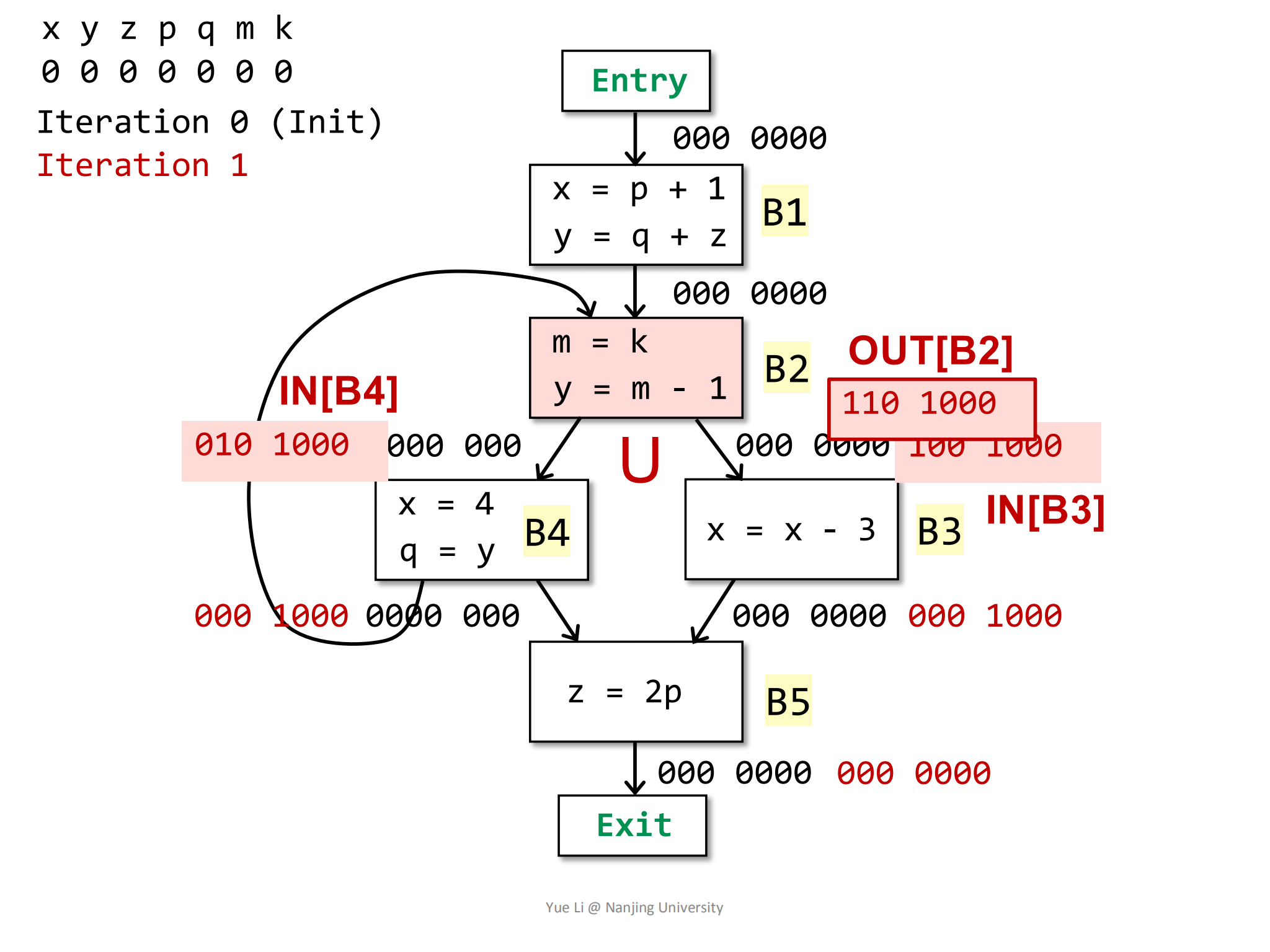
然后根据transfer function求解
IN[B2],这里需要注意变量m即发生了重定义,又被使用了,但是重定义发生在使用之前,所以变量在程序点IN[B2]处是dead的,只有变量k是live的:1
2
3
4
5
6
7
8use[B2] = { k } = 000 0001
OUT[B2] = 110 1000
def[B2] = { y, m } = 010 0010
IN[B2] = use[B2] U (OUT[B2] - def[B2])
= 000 0001 U (110 1000 - 010 0010)
= 000 0001 U 100 1000
= 100 1001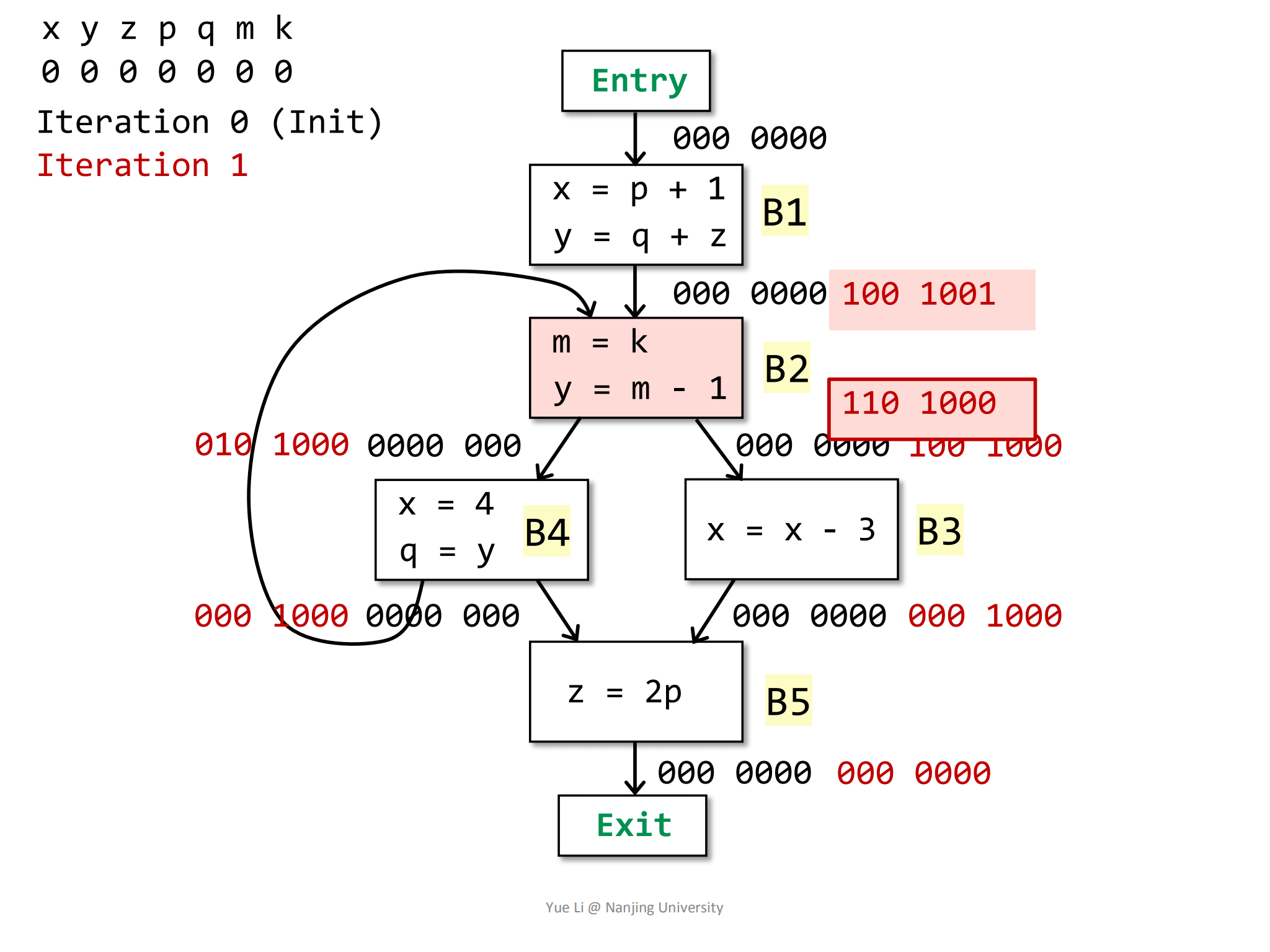
最后是求解B1块的相关信息:
1
2OUT[B1] = IN[B2]
= 100 1001然后是根据transfer function求解
IN[B1]:1
2
3
4
5
6
7
8use[B1] = { p, q, z } = 001 1100
OUT[B1] = 100 1001
def[B2] = { x, y } = 110 0000
IN[B1] = use[B1] U (OUT[B1] - def[B2])
= 001 1100 U (100 1001 - 110 0000)
= 001 1100 U 000 1001
= 001 1101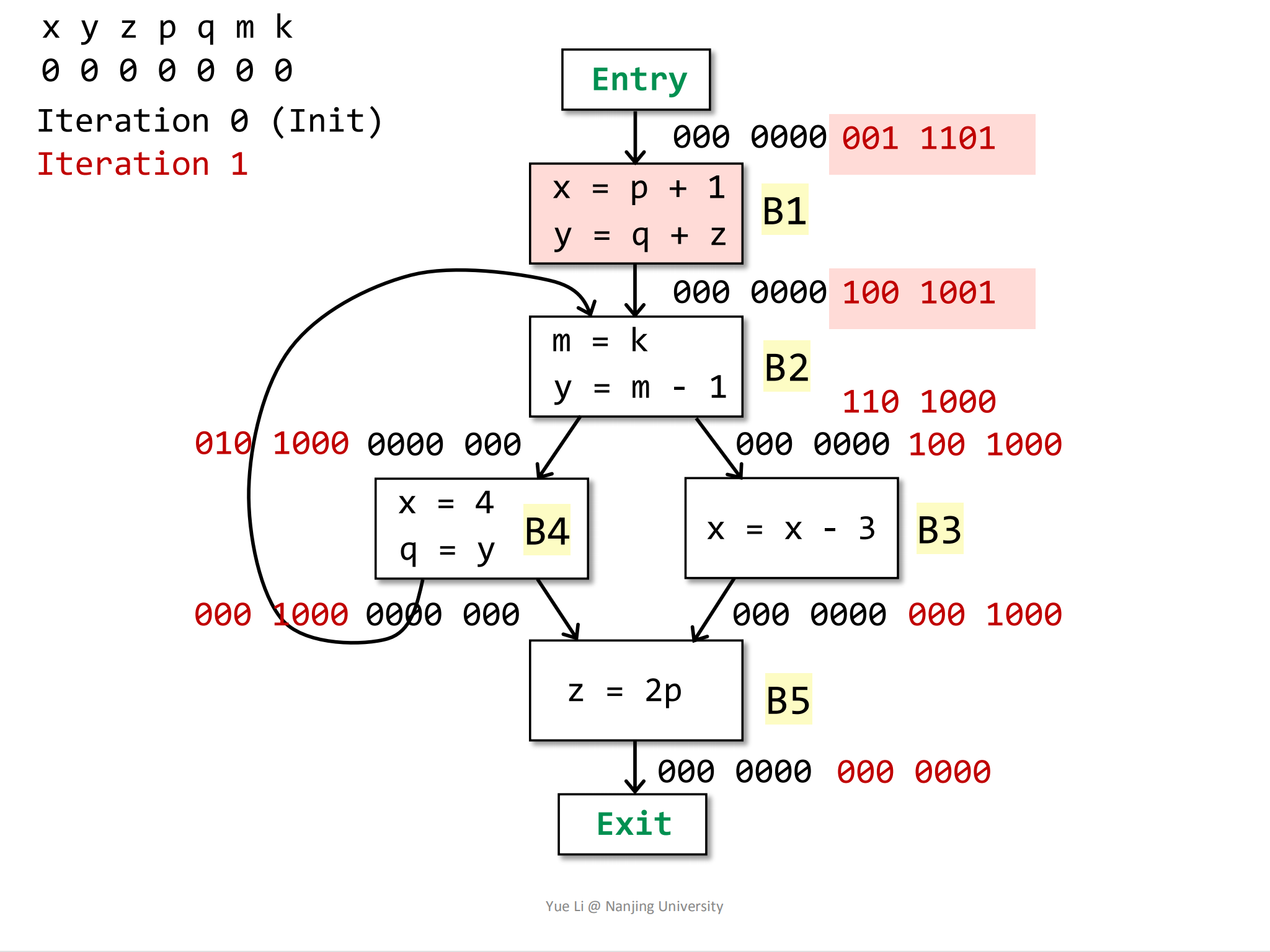
第一轮迭代到这里已经结束了,但是算法并没有结束,因为IN[B1],IN[B2],IN[B3],IN[B4]和IN[B5]都发生了改变。
第二轮迭代
第二轮迭代也是从B5块开始:
1
2OUT[B5] = IN[exit]
= 000 0000然后利用
OUT[B5]计算IN[B5]:1
2
3
4
5
6
7
8use[B5] = { p } = 000 1000
OUT[B5] = 000 0000
def[B5] = { z } = 001 0000
IN[B5] = use[B5] U (OUT[B5] - def[B5])
= 000 1000 U (000 0000 - 001 0000)
= 000 1000 U 000 0000
= 000 1000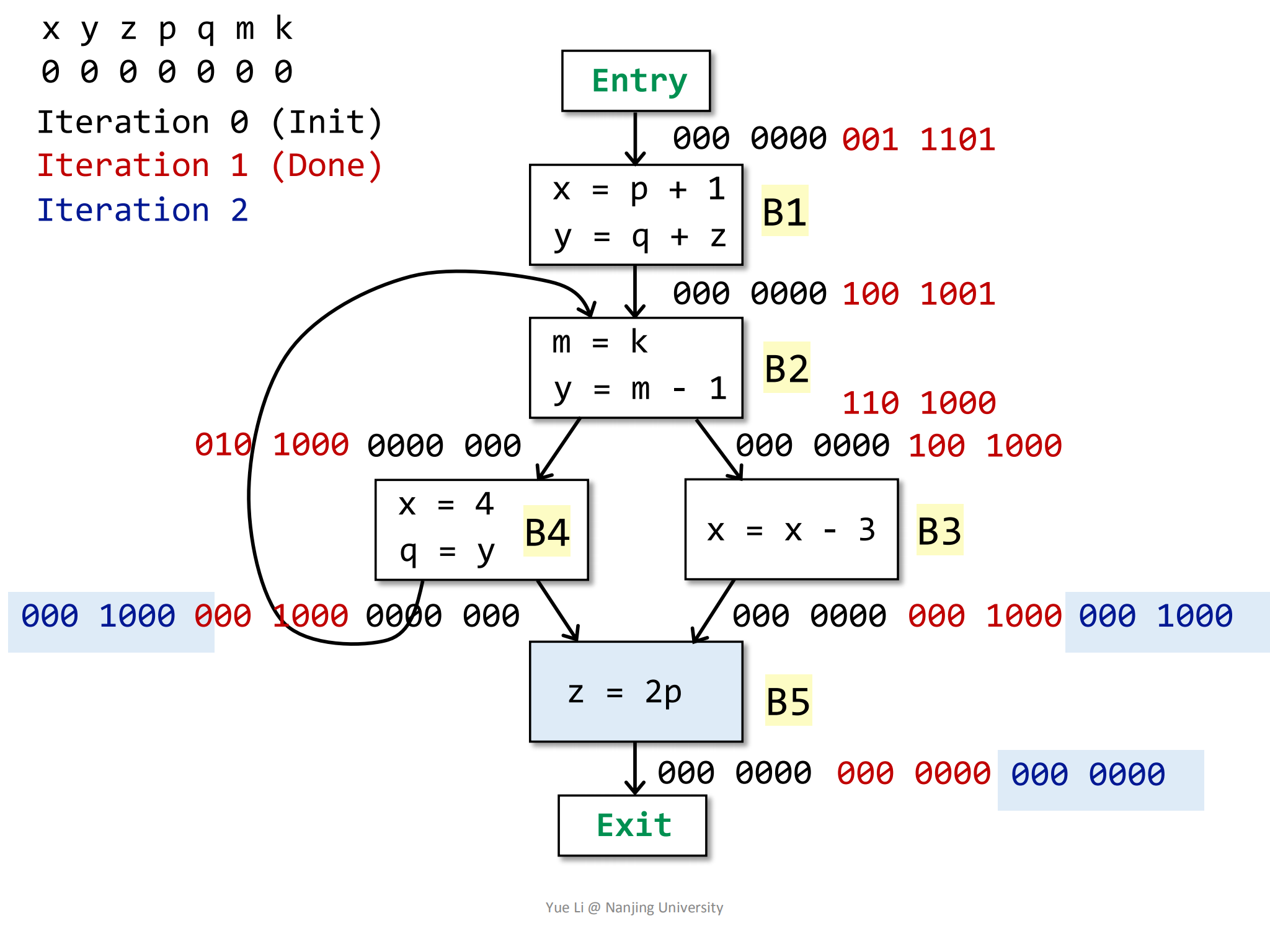
相较于上一轮迭代结果,
IN[B5]没有发生变化。然后是B3块,首先根据控制流信息计算
OUT:1
2OUT[B3] = IN[B5]
= 000 1000然后根据转换函数计算
IN,变量x是先被使用后被重新定义的,所以对于程序点IN[B3]来说,变量x是live的:1
2
3
4
5
6
7
8use[B3] = { x } = 100 0000
OUT[B3] = 000 1000
def[B3] = { x } = 100 0000
IN[B3] = use[B3] U (OUT[B3] - def[B3])
= 100 0000 U (000 1000 - 100 0000)
= 100 0000 U 000 1000
= 100 1000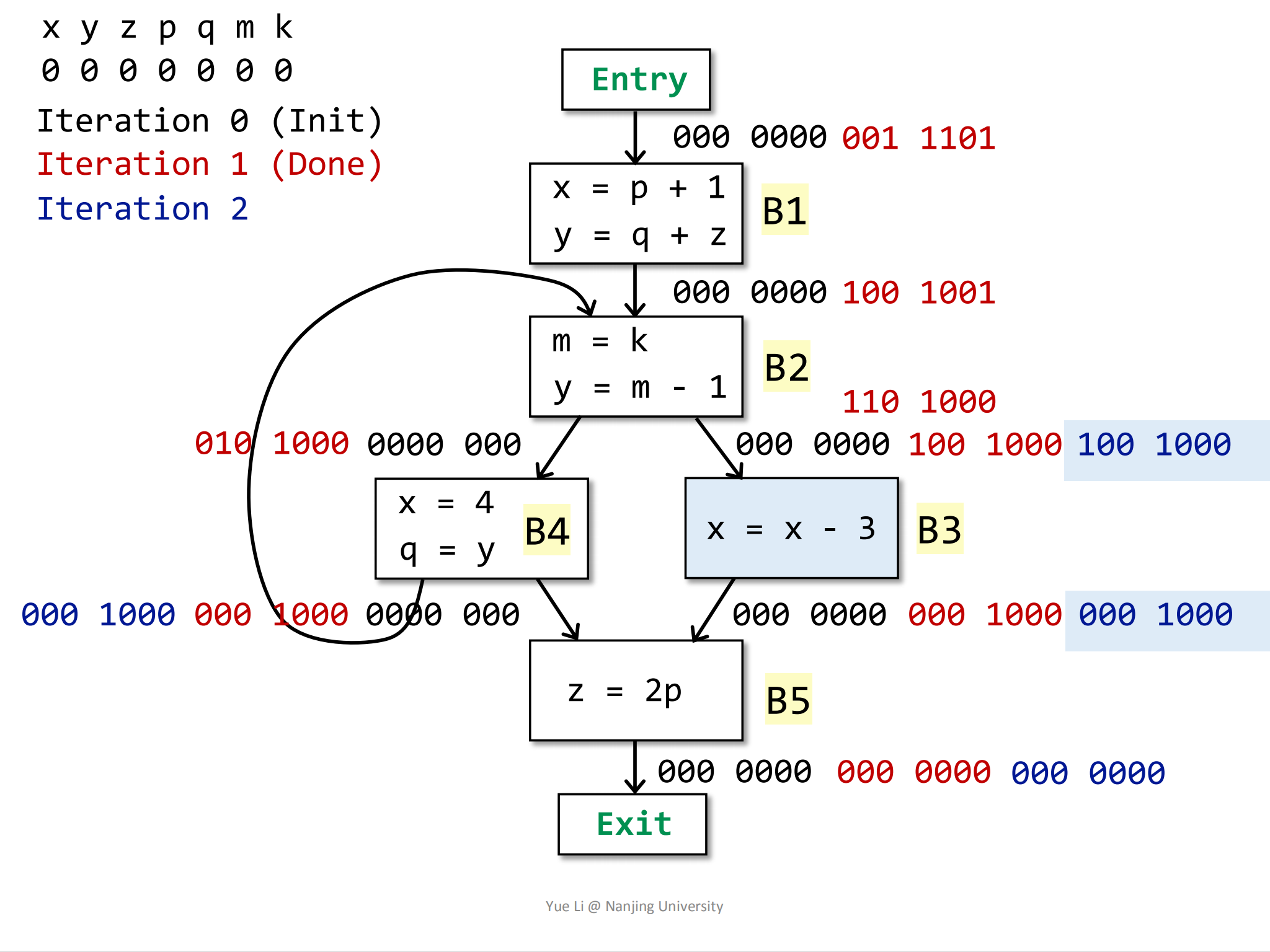
相较于上一轮迭代结果,
IN[B3]也没有发生变化。然后计算B4:
1
2
3OUT[B4] = IN[B2] U IN[B5]
= 100 1001 U 000 1000
= 100 1001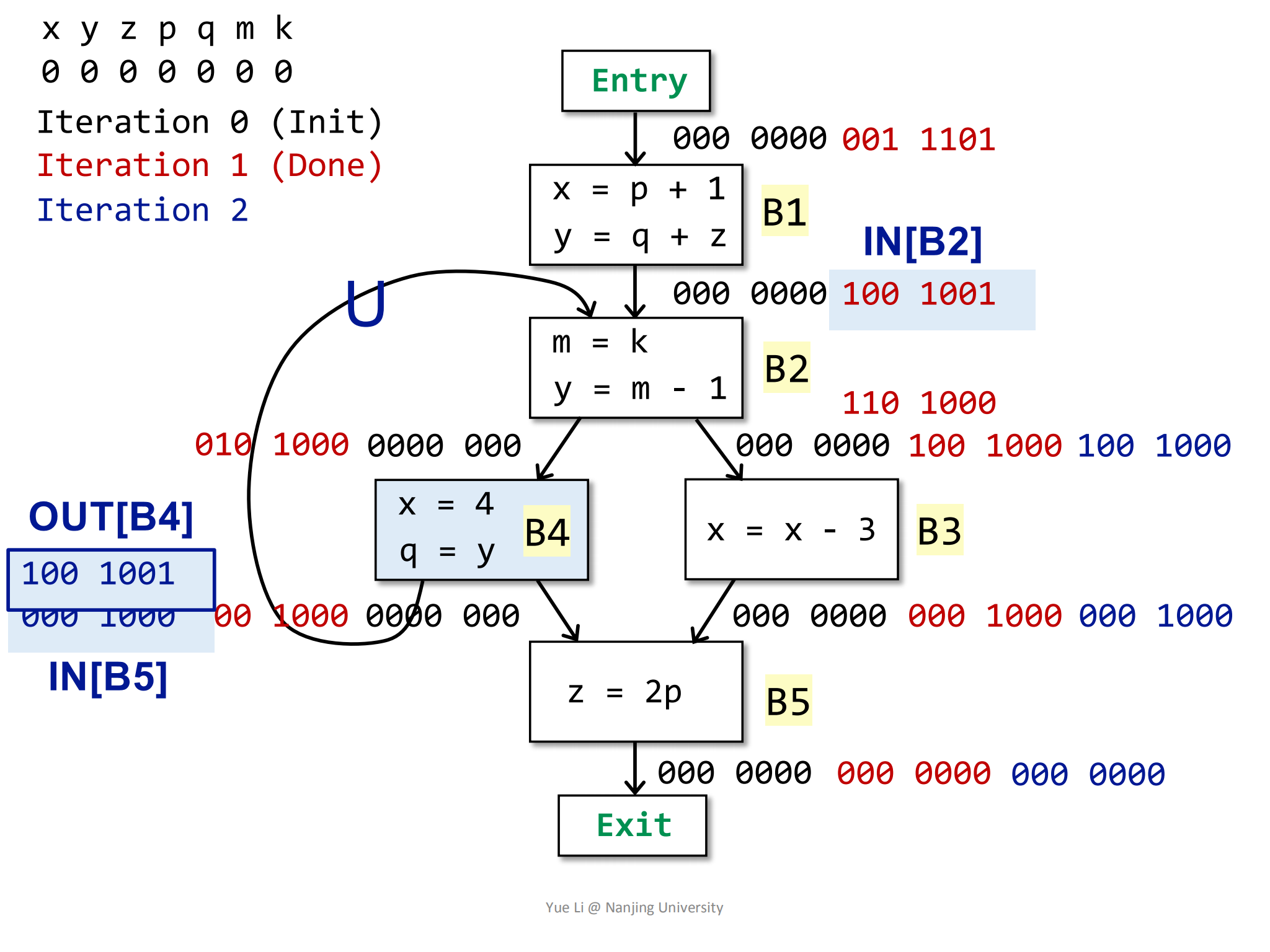
然后计算
IN[B4]:1
2
3
4
5
6
7
8use[B4] = { y } = 010 0000
OUT[B4] = 100 1001
def[B4] = { x, q } = 100 0100
IN[B4] = use[B4] U (OUT[B4] - def[B4])
= 010 0000 U (100 1001 - 100 0100)
= 010 0000 U 000 1001
= 010 1001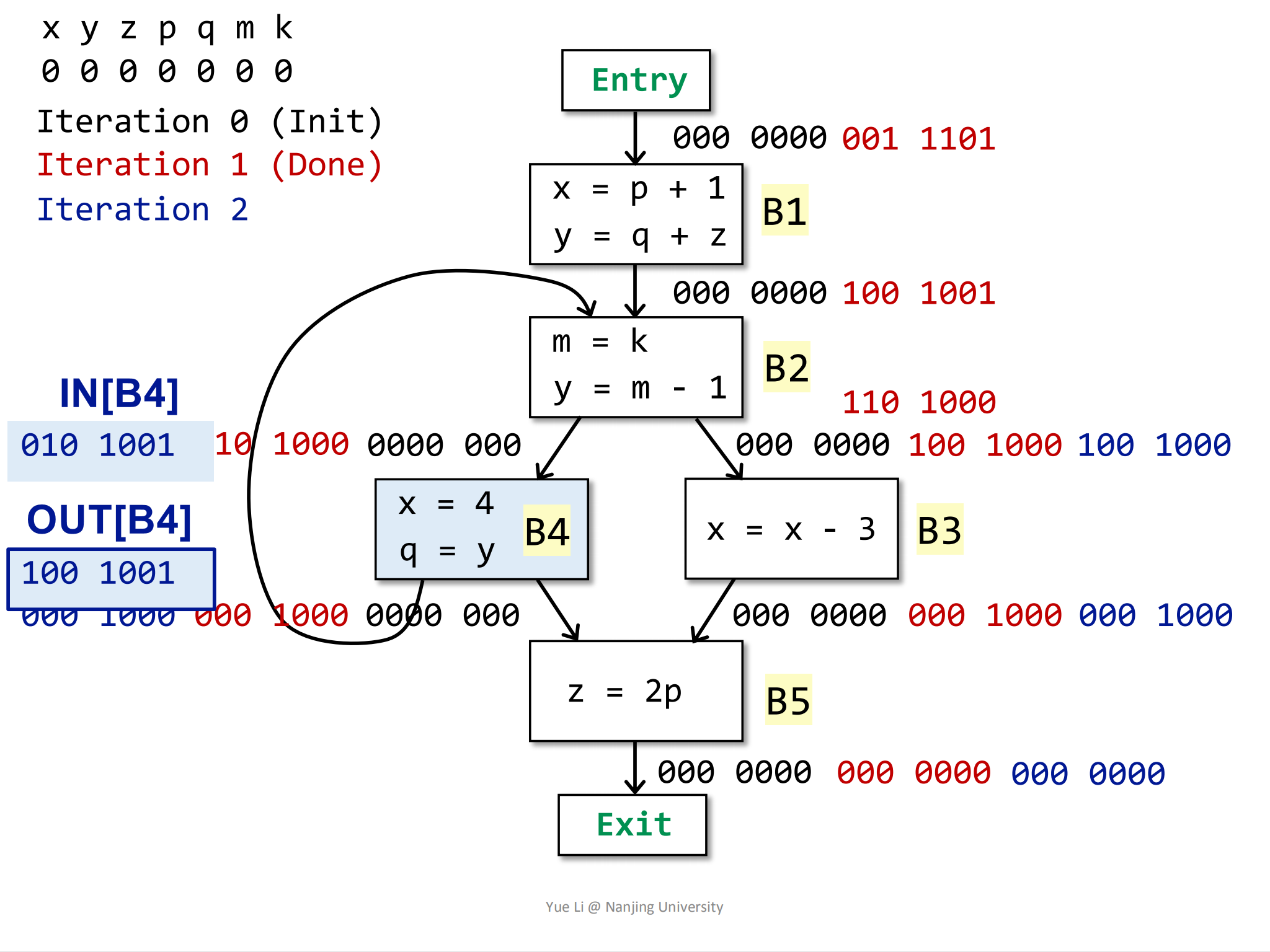
相较于前一次的结果,
IN[B4]发生了改变。然后计算B2块,它的后继节点为
B3和B4:1
2
3OUT[B2] = IN[B3] U IN[B4]
= 100 1000 U 010 1001
= 110 1001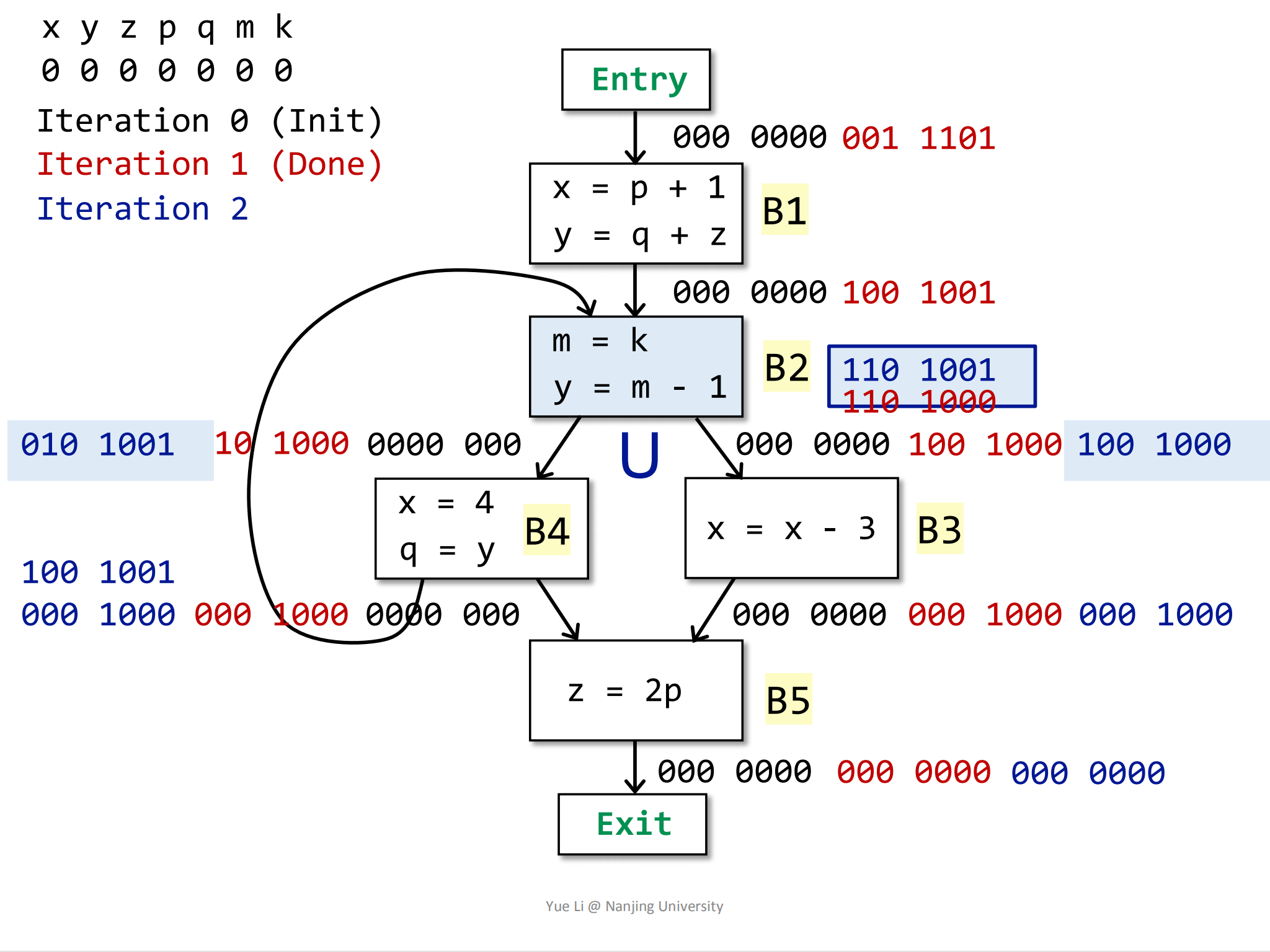
然后根据transfer function计算IN信息,要注意的是变量m是先被重新定义,然后被使用的,所以对于程序点
IN[B2]来说,变量是dead的,所以在程序点IN[B2]处,只有变量k是live的:1
2
3
4
5
6
7
8use[B2] = { k } = 000 0001
OUT[B2] = 110 1001
def[B2] = { m, y } = 010 0010
IN[B2] = use[B2] U (OUT[B2] - def[B2])
= 000 0001 U (110 1001 - 010 0010)
= 000 0001 U 100 1001
= 100 1001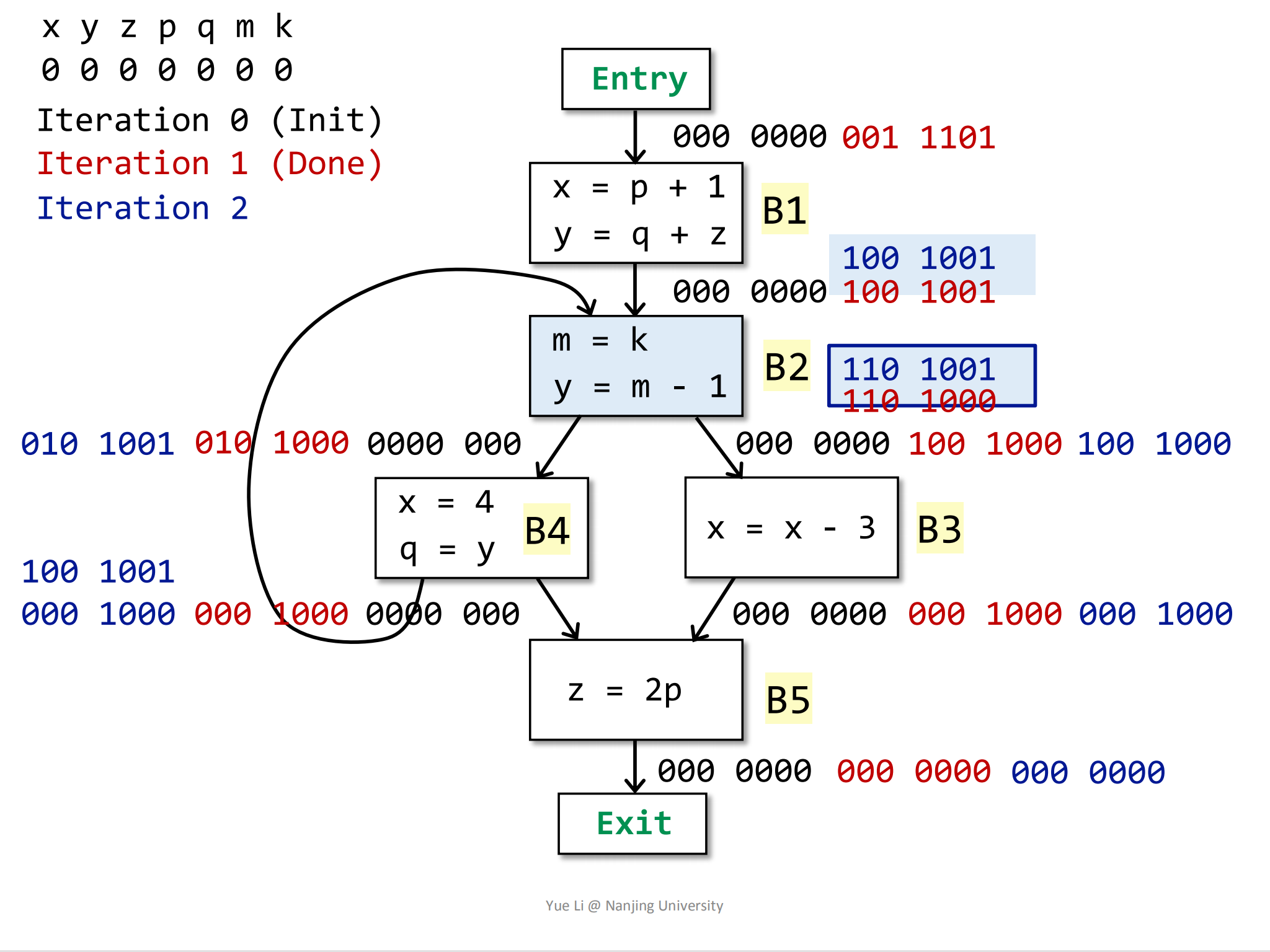
相较于上一次的结果,
IN[B2]也没有发生变化。最后计算B1块的IN和OUT:
1
2OUT[B5] = IN[B2]
= 100 1001然后计算IN,变量p,q和z被使用了:
1
2
3
4
5
6
7
8use[B1] = { p, q, z } = 001 1100
OUT[B1] = 100 1001
def[B1] = { x, y } = 110 0000
IN[B1] = use[B1] U (OUT[B1] - def[B1])
= 001 1100 U (100 1001 - 110 0000)
= 001 1100 U 000 1001
= 001 1101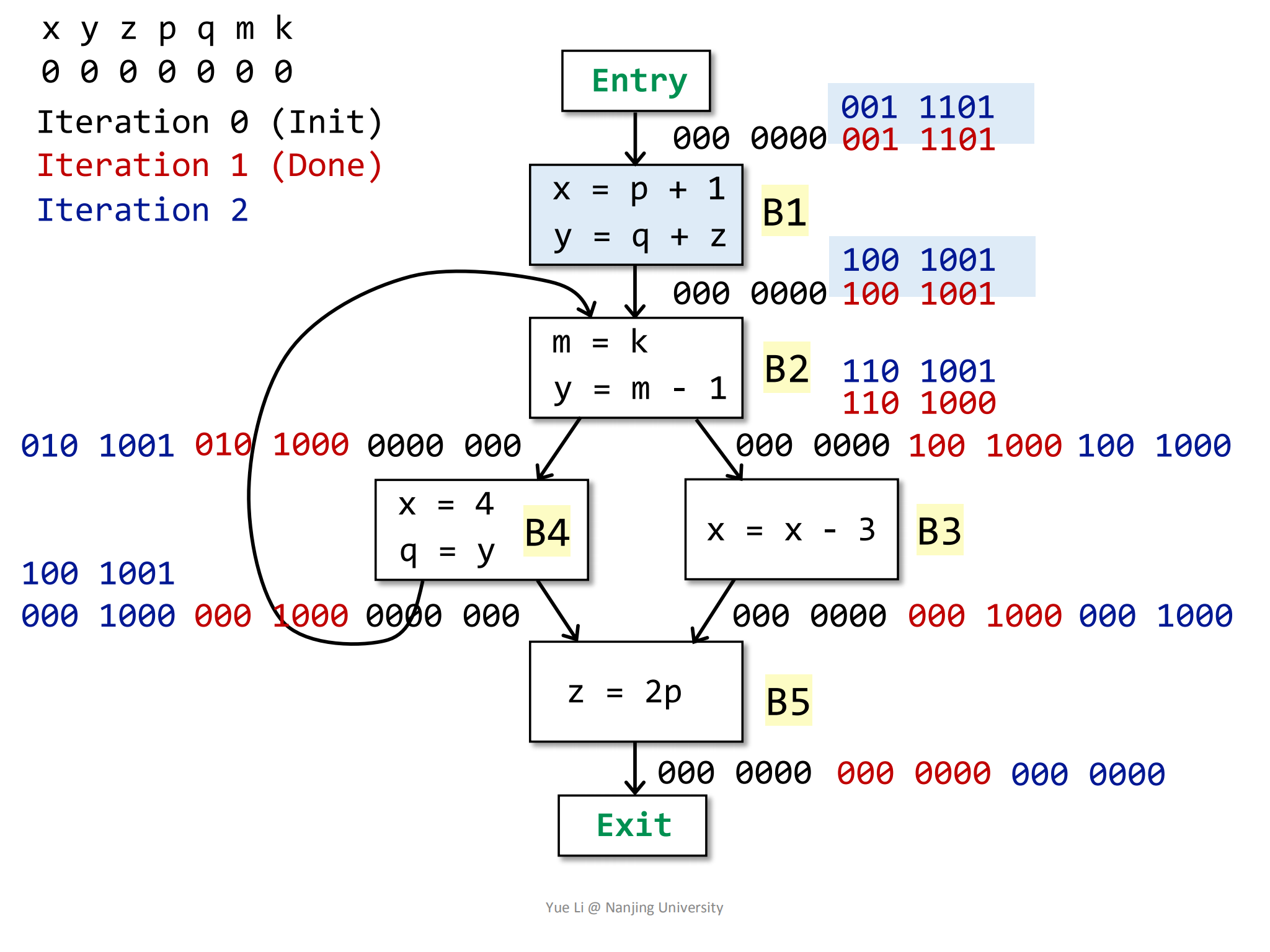
相较于上一轮的结果,
IN[B1]也没有发生变化。
所以在第二轮迭代结束之后,只有IN[B4]发生了变化。
第三轮迭代
按照前面的方式,第三次结束之后,没有一个Block的IN发生变化:
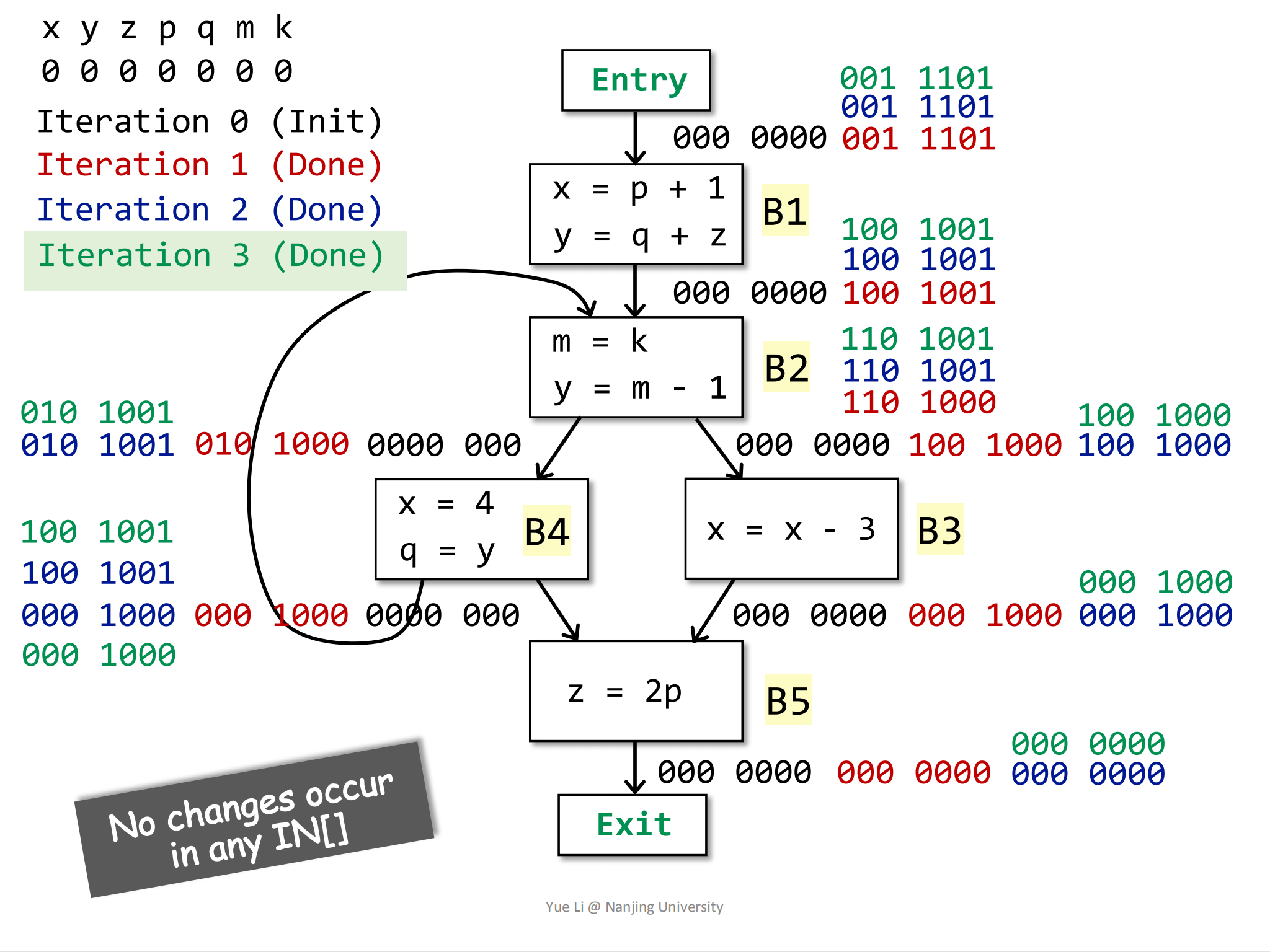
迭代到此结束。
小结
Live Variables算法到这里就结束了,下一节课要开始学习Available Expressions Analysis。
至于算法为什么最后能停下来,原因和上一节的定义可达分析中迭代算法能停下来的原因是一样的,对于每一个BB块来说,use[B]和def[B]都是不变的,唯一会发生变化的就是OUT[B]。OUT[B]是由它后继节点的IN来决定的,在OUT[B]中,只会发生0->1,1->1或是0->0这三种情况,所以OUT[B]会慢慢收敛成一个不动点。所以最后IN[B]也会随着OUT[B]不再变化而变成也给不动点,最后算法就能够停下来了。