前言
- Reaching Definitions Analysis
- Live Variables Analysis
- Available Expressions Analysis
前面两节学习了Reaching Definitions Analysis(可达定义分析)和Live Variables Analysis(存活变量分析,可能这样翻译不太准确),这两种分析方法都是may analysis。
本文要学习的是最后的Available Expression Analysis(可替换表达式分析),这是一种must analysis。
Available Expressions Analysis定义

课程ppt上给出的定义是这样的:
An expression
x op yis available at program point p if (1) all paths from the entry to p must pass through the evaluation ofx op y,and (2) after the last evaluation ofx op y, there is no redefinition ofx op y
翻译成我可以理解的语言就是:
表达式
x op y在程序点p被认为是可用的表达式需要满足两个条件:(1) 从entry到程序点p的所有路径都必须经过表达式
x op y(2) 最后一次使用表达式
x op y之后,操作数x和y不能被重定义
条件(1)比较好理解,比如从entry到程序点p有100条路径,那么这100条路径都要经过表达式x op y。
也就是说,如果在程序点p处表达式是available的,那么就可以用最后一次的计算结果来替换表达式x op y。
Available Expressions Analysis可以用来检测全局通用表达式。
Available Expressions Analysis理解
假设现在有100个expressions,按照顺序命名为E1,E2,E3,...,E100,最后用一个bit vector来表示:

transfer function
假设现在有如下图所示的CFG片段,有个BasicBlock,对应的表达式为x op y:

gen:
x op y是新的expression,所以得到gen[B] = { x op y }kill:
a = x op y,变量a被重定义了,所以表达式a + b被kill了,kill[B] = { a + b }transfer function:得到的转换函数为:
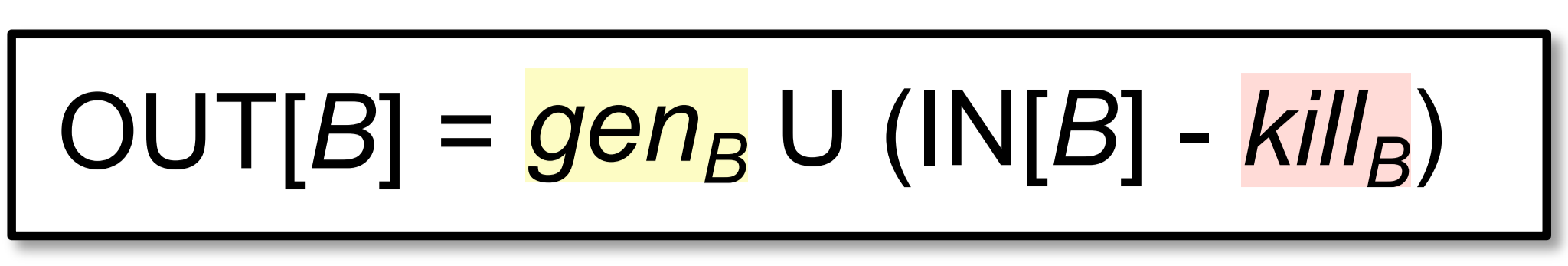
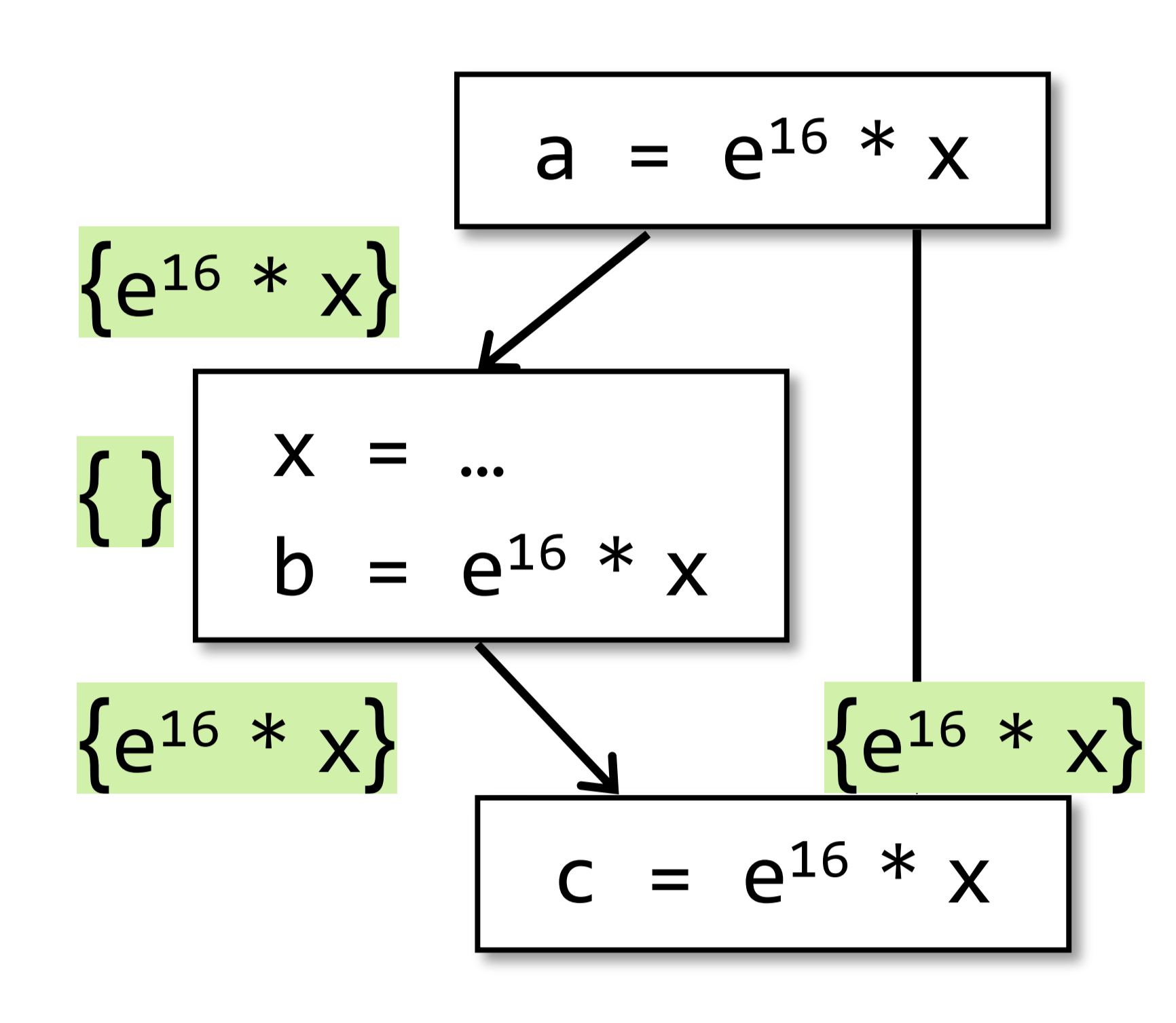
下图的例子中,从表达式a = e^16 * x到表达式c = e^16 * x,无论走哪条路径,计算e^16 * x,都可以用它的last expression值来替代:
根据control flow信息,可以得到IN[B]的计算公式:

因为Available Expressions Analysis是must analysis,所以这里的符号是∩,需要对BasicBlock的所有前驱块P的OUT[P]取一个交集。这样才能控制所有情况下都满足。
对于may analysis来说,可以存在误报,即false positive,但是不可以有漏报,即false negative;但是must analysis正好相反,可以存在漏报,但是不可以有误报。
Available Expressions Analysis算法
下图是算法伪代码。

首先进行初始化,边界值的OUT,即OUT[entry] = ∅,除了entry块之外,其余块的OUT都是U(用数学符号来表示,就是1111…111)。接下来进行的迭代和之前两种算法类似,就不再赘述了。
Available Expressions Analysis实例
现在有一个程序的控制流,涉及5个BasicBlocks,共有5个表达式:
p - 1
z / 5
2 * y
e^7 * x
y + 3
首先进行初始化,根据迭代算法,OUT[entry] = 00000,其余块OUT均初始化为U,得到OUT[B\entry] = 11111:
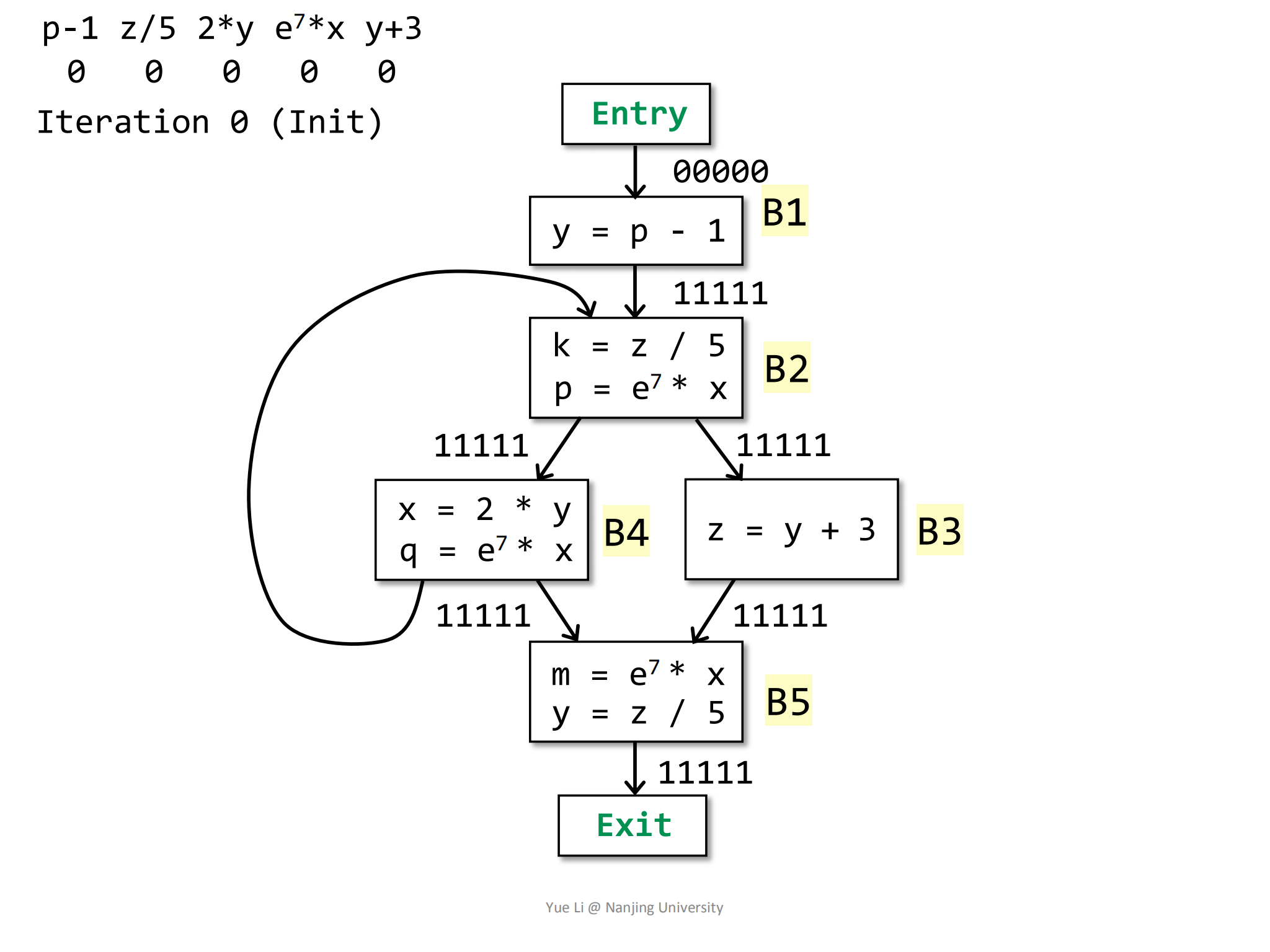
第一轮迭代
根据控制流信息计算
IN[B1]:1
2IN[B1] = OUT[entry]
= 0 0000然后根据transfer function计算
OUT[B1]:1
2
3
4
5
6
7gen[B1] = { p - 1 } = 1 0000
IN[B1] = 0 0000
kill[B1] = { 2 * y, y + 3 } = 0 0101
OUT[B1] = gen[B1] U (IN[B1] - kill[B1])
= 1 0000 U (0 0000 - 0 0101)
= 1 0000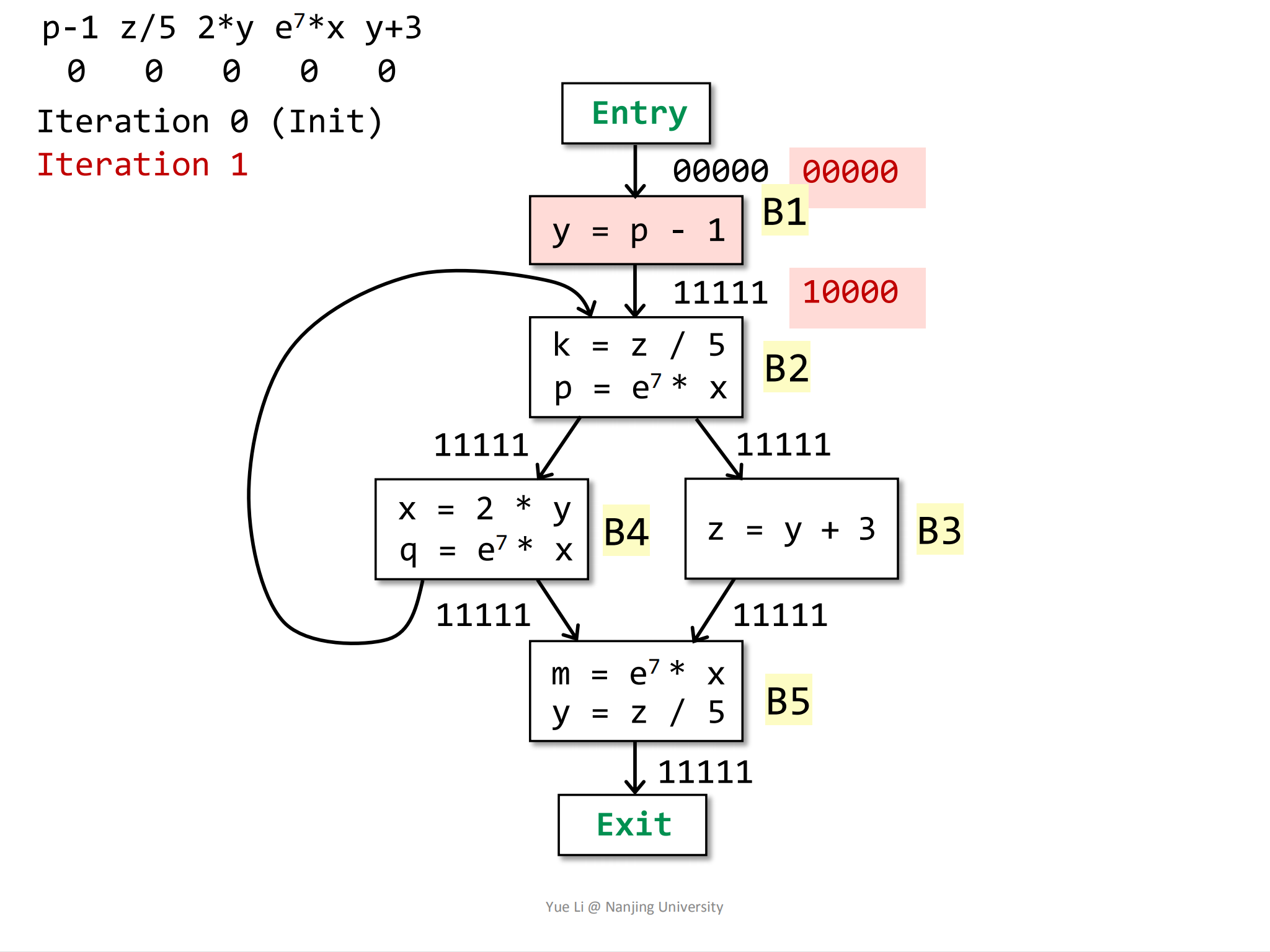
根据控制流信息计算
IN[B2],B2块的前驱块为B1和B4:1
2
3IN[B2] = OUT[B1] ∩ OUT[B4]
= 1 0000 ∩ 1 1111
= 1 0000从这里我们已经可以感觉到为什么初始化时
OUT[entry\B]块需要被设置为U,如果也是设置为∅,那么IN就永远都是∅了。接着根据转换函数计算
OUT[B2],因为有一个statement是p = e^7 * x,所以表达式p - 1被kill了:1
2
3
4
5
6
7gen[B2] = { z / 5, e^7 * x} = 0 1010
IN[B2] = 1 0000
kill[B2] = { p - 1 } = 1 0000
OUT[B2] = gen[B2] U (IN[B2] - kill[B2])
= 0 1010 U (1 0000 - 1 0000)
= 0 1010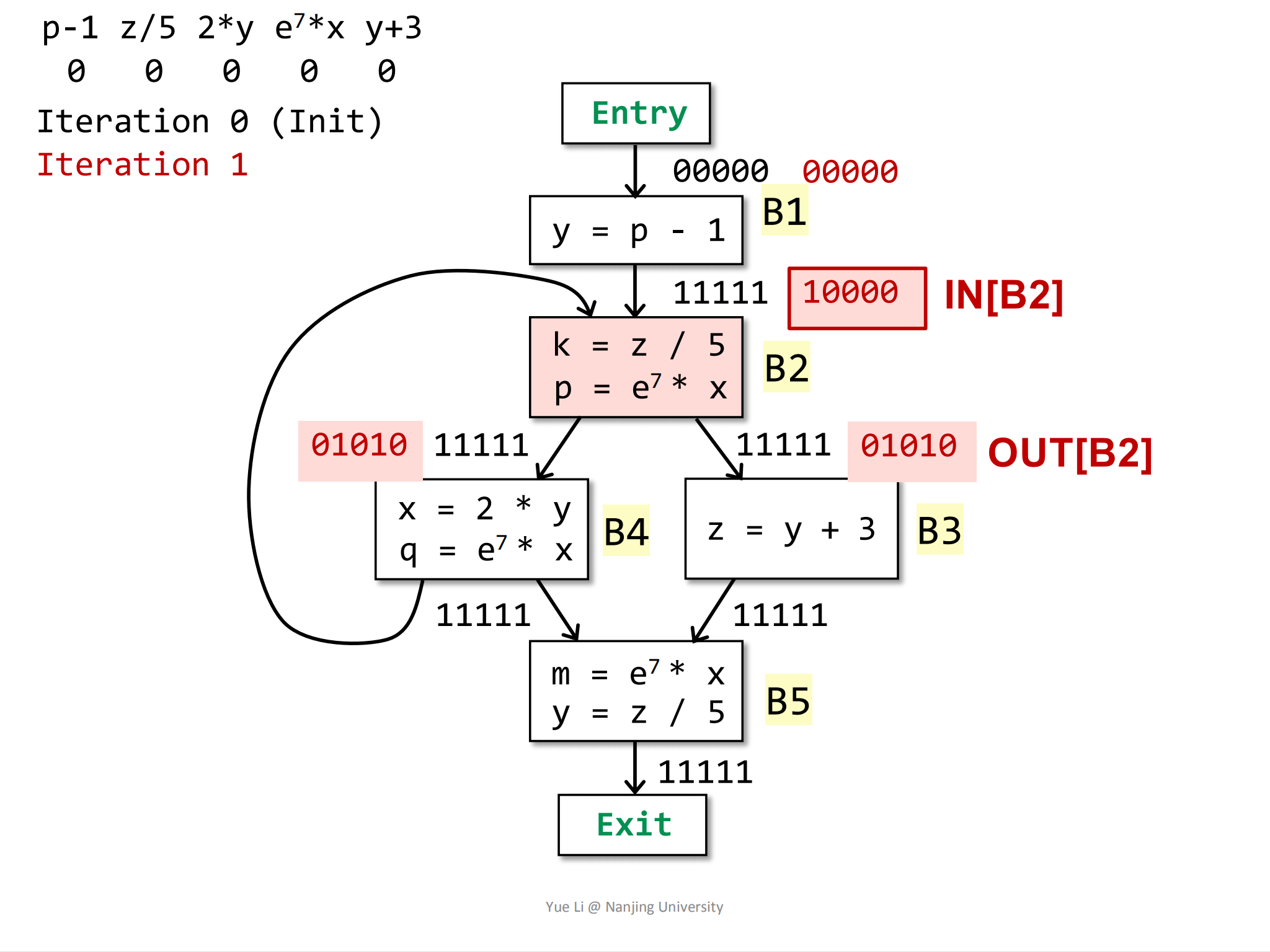
接着计算B3块的
IN,它的前驱块只有B2,所以:1
2IN[B3] = OUT[B2]
= 0 1010然后根据transfer function计算
OUT,B3块的statement为z = y + 3,所以与变量z被重定义了,所以与变量z相关的表达式z / 5被kill了:1
2
3
4
5
6
7
8gen[B3] = { y + 3 } = 0 0001
IN[B3] = 0 1010
kill[B3] = { z / 5 } = 0 1000
OUT[B3] = gen[B3] U (IN[B3] - kill[B3])
= 0 0001 U (0 1010 - 0 1000)
= 0 0001 U 0 0010
= 0 0011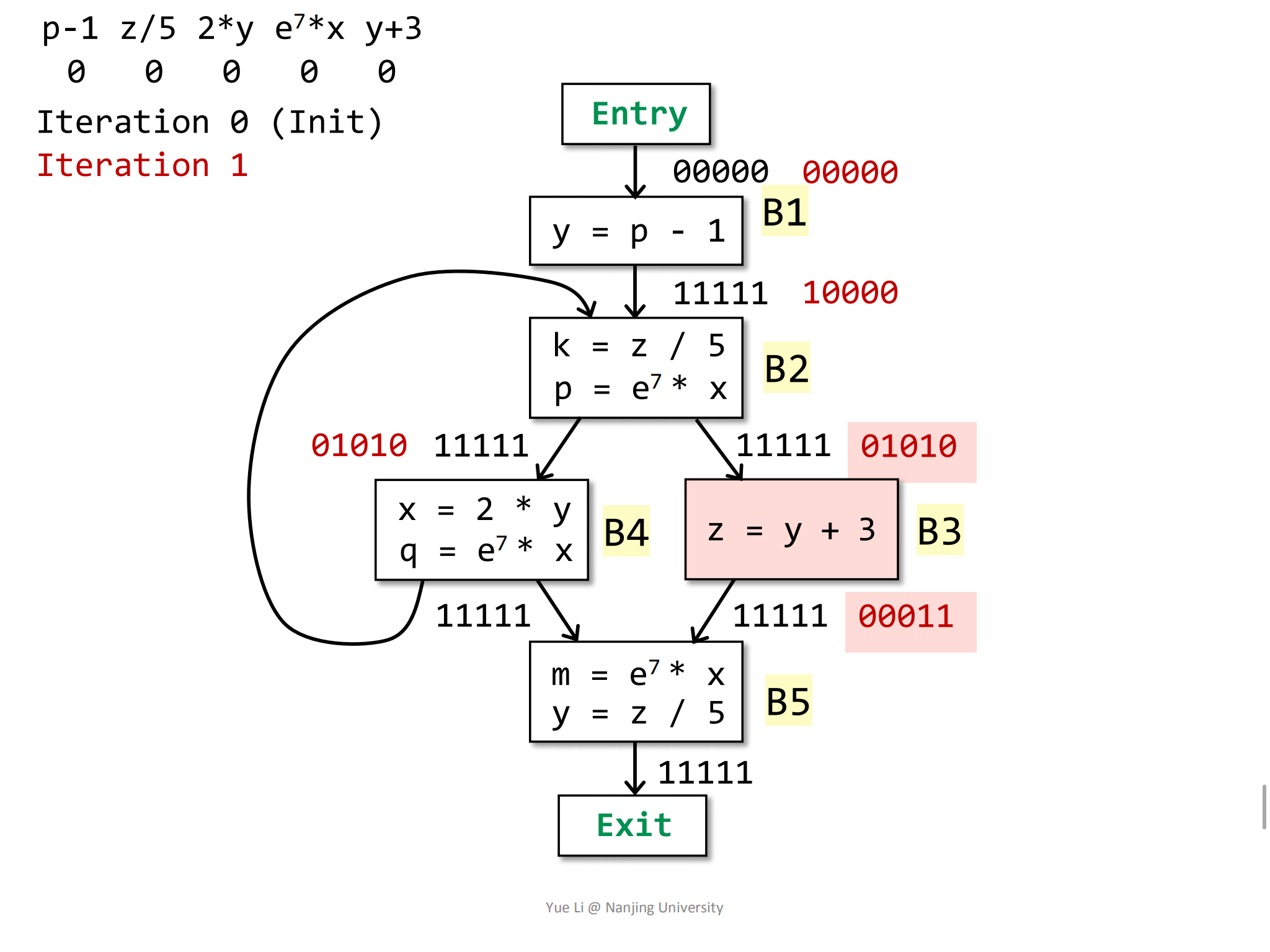
然后计算B4块的
IN[B4],它的前驱块也是B2:1
2IN[B4] = OUT[B2]
= 0 1010然后计算
OUT[B4],变量x和变量q发生了重定义,所以与它们相关的表达式需要被kill掉,变量q没有与之相关的表达式,所以可以不去管,与变量x相关的表达式为e^7 * x:1
2
3
4
5
6
7
8gen[B4] = { 2 * y, e^7 * x } = 0 0110
IN[B4] = 0 1010
kill[B4] = { e^7 * x } = 0 0010
OUT[B4] = gen[B4] U (IN[B4] - kill[B4])
= 0 0110 U (0 1010 - 0 0010)
= 0 0110 U 0 1000
= 0 1110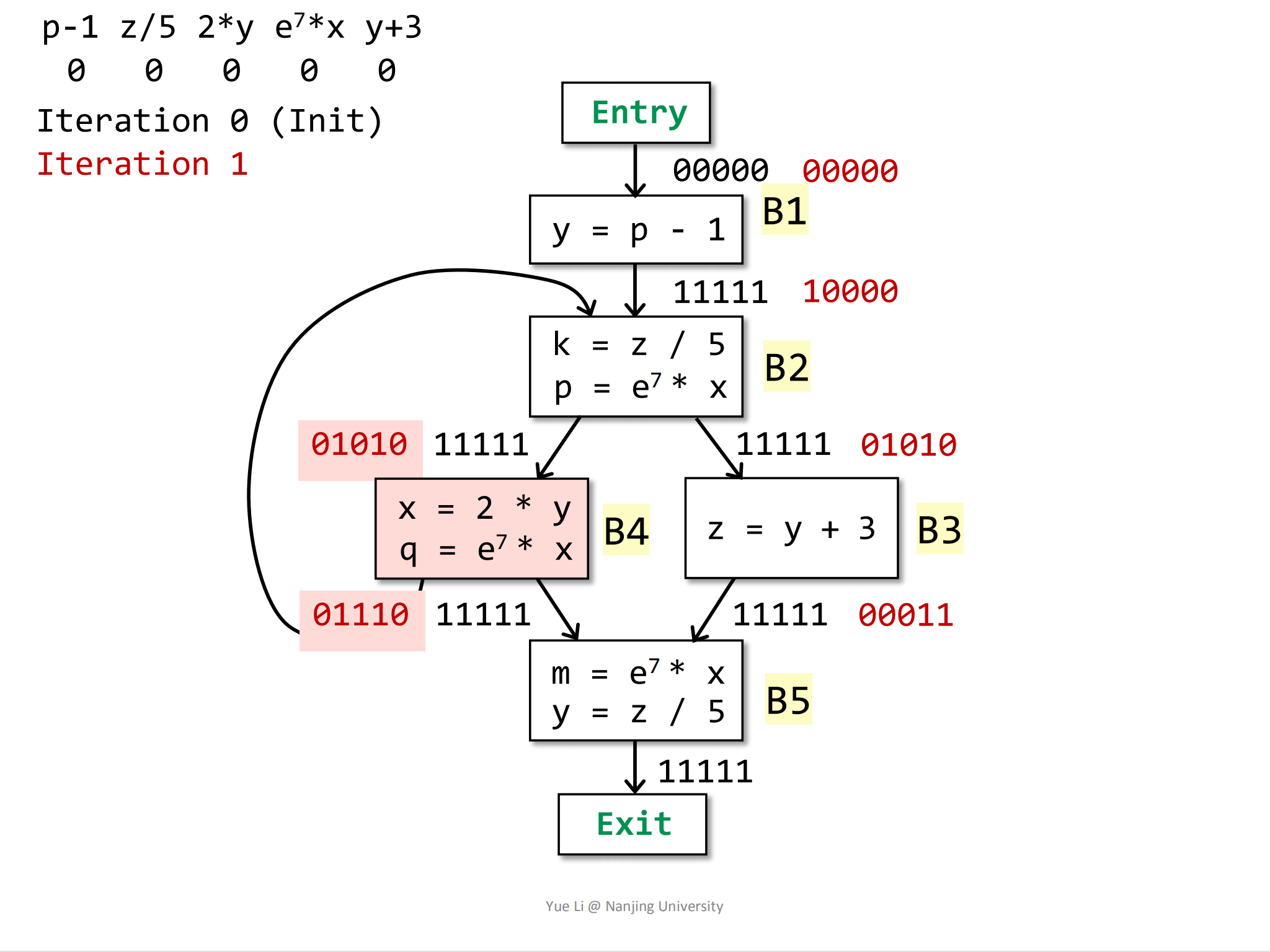
最后一个BasicBlock块是B5,它的前驱块为B3和B4:
1
2
3IN[B5] = OUT[B3] ∩ OUT[B4]
= 0 1110 ∩ 0 0011
= 0 0010然后计算
OUT,变量y被重新定义,所以表达式2 * y和y + 3被kill掉:1
2
3
4
5
6
7
8gen[B5] = { e^7 * x, z / 5 } = 0 1010
IN[B5] = 0 0010
kill[B5] = 0 0101
OUT[B5] = gen[B5] U (IN[B5] - kill[B5])
= 0 1010 U (0 0010 - 0 0101)
= 0 1010 U 0 0010
= 0 1010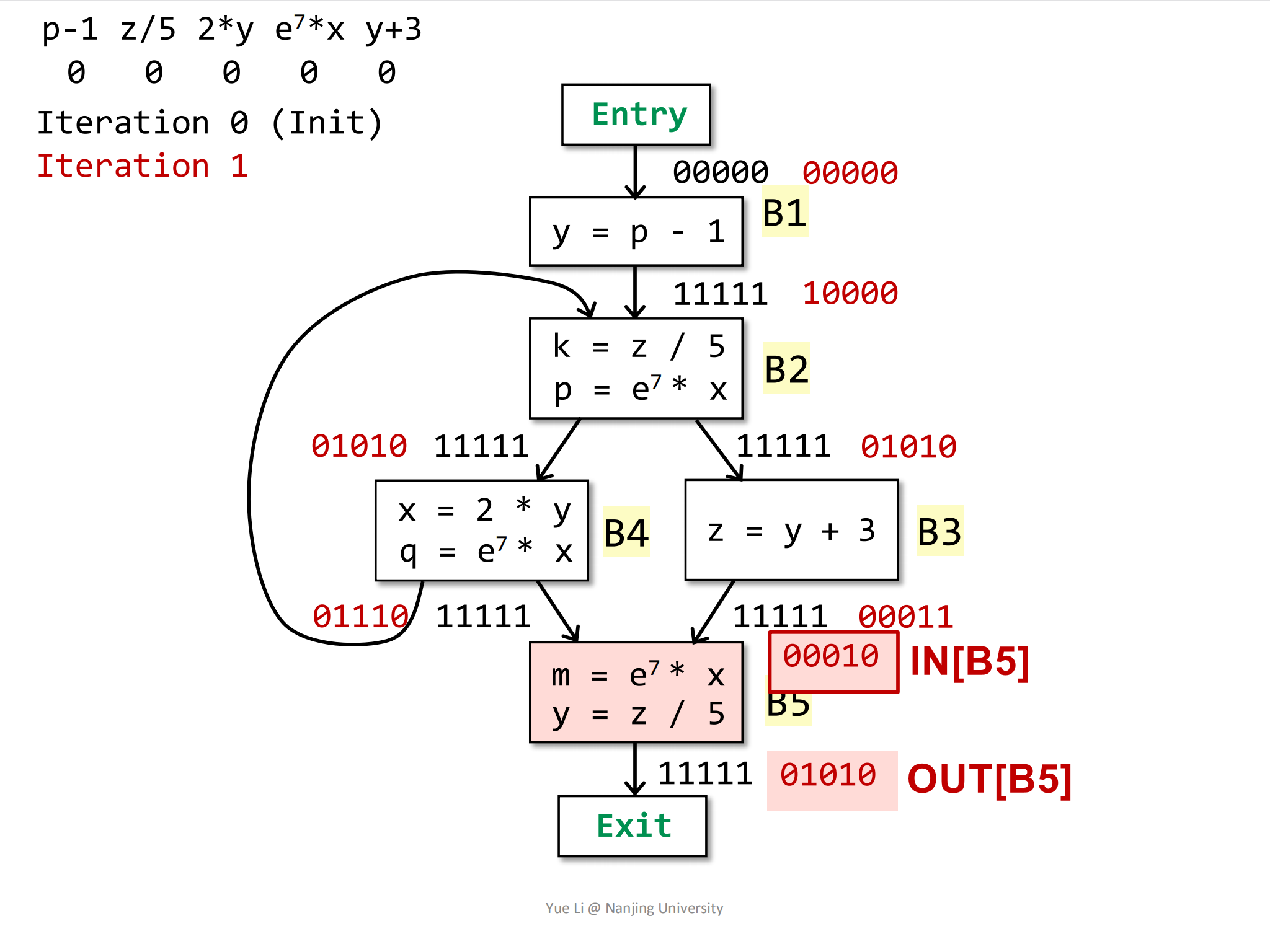
第一轮遍历结束后,OUT[B1],OUT[B2],OUT[B3],OUT[B4]和OUT[B5]都发生了变化,所以迭代继续。
第二轮迭代
还是从B1块开始,前驱块为entry:
1
2IN[B1] = OUT[entry]
= 0 0000B1块对变量y进行了重定义,所以变量
y相关的表达式2 * y和y + 3都被kill了,同时,新生成的表达式为p - 1:1
2
3
4
5
6
7
8gen[B1] = { p - 1 } = 1 0000
IN[B1] = 0 0000
kill[B1] = { 2 * y, y + 3 } = 0 0101
OUT[B1] = gen[B1] U (IN[B1] - kill[B1])
= 1 0000 U (0 0000 - 0 0101)
= 1 0000 U 0 0000
= 1 0000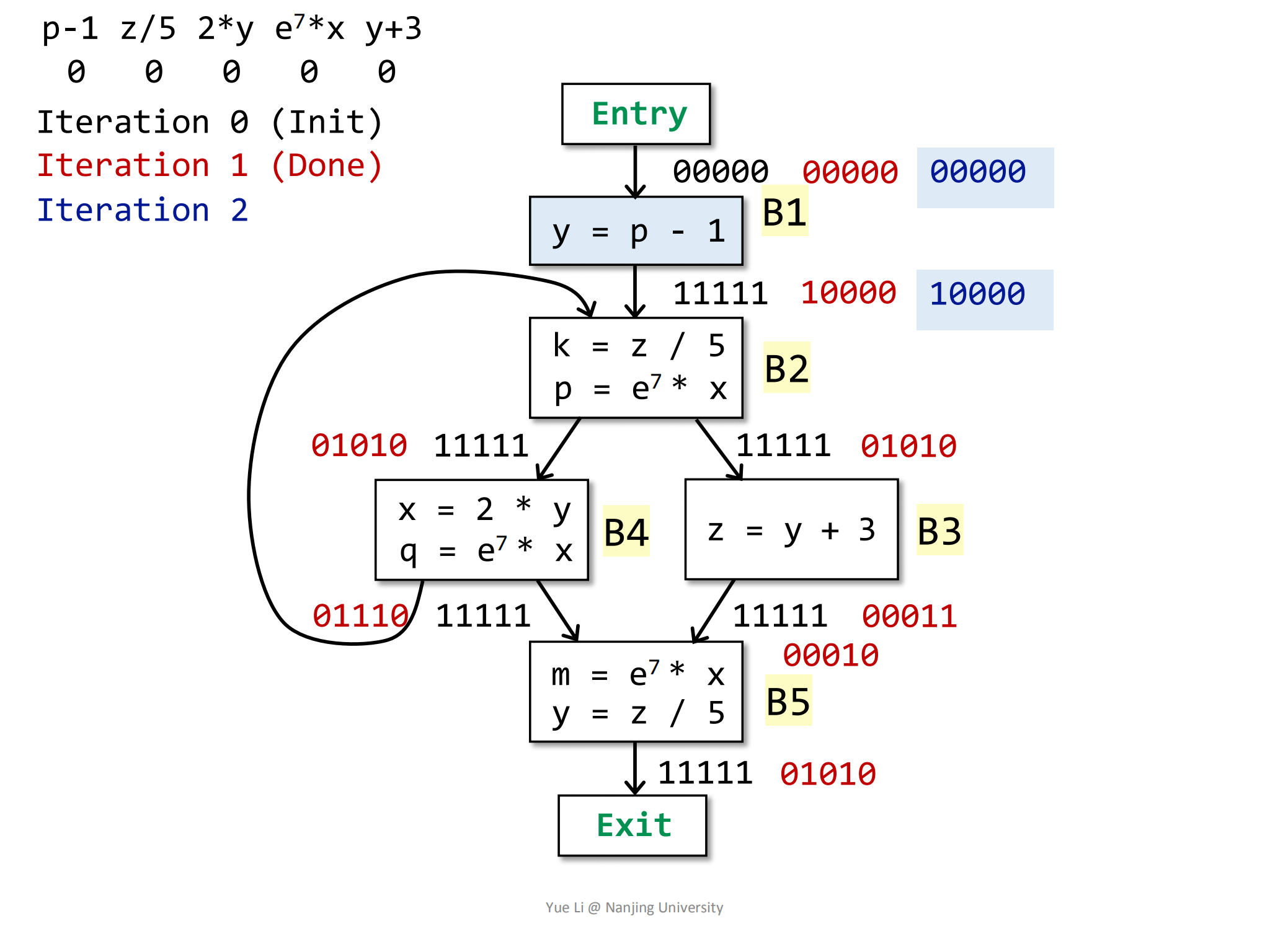
相比于上一次迭代结果,
OUT[B1]没有发生变化,因为entry块没有发生变化,而gen和kill都是由statements来决定的,statements不会变,所以gen和kill也不会发生变化,因此OUT[B1]也不会发生变化,可以看到,OUT的结果集已经开始收敛了。然后计算B2块的
IN:1
2
3IN[B2] = OUT[B1] ∩ OUT[B4]
= 1 0000 ∩ 0 1110
= 0 0000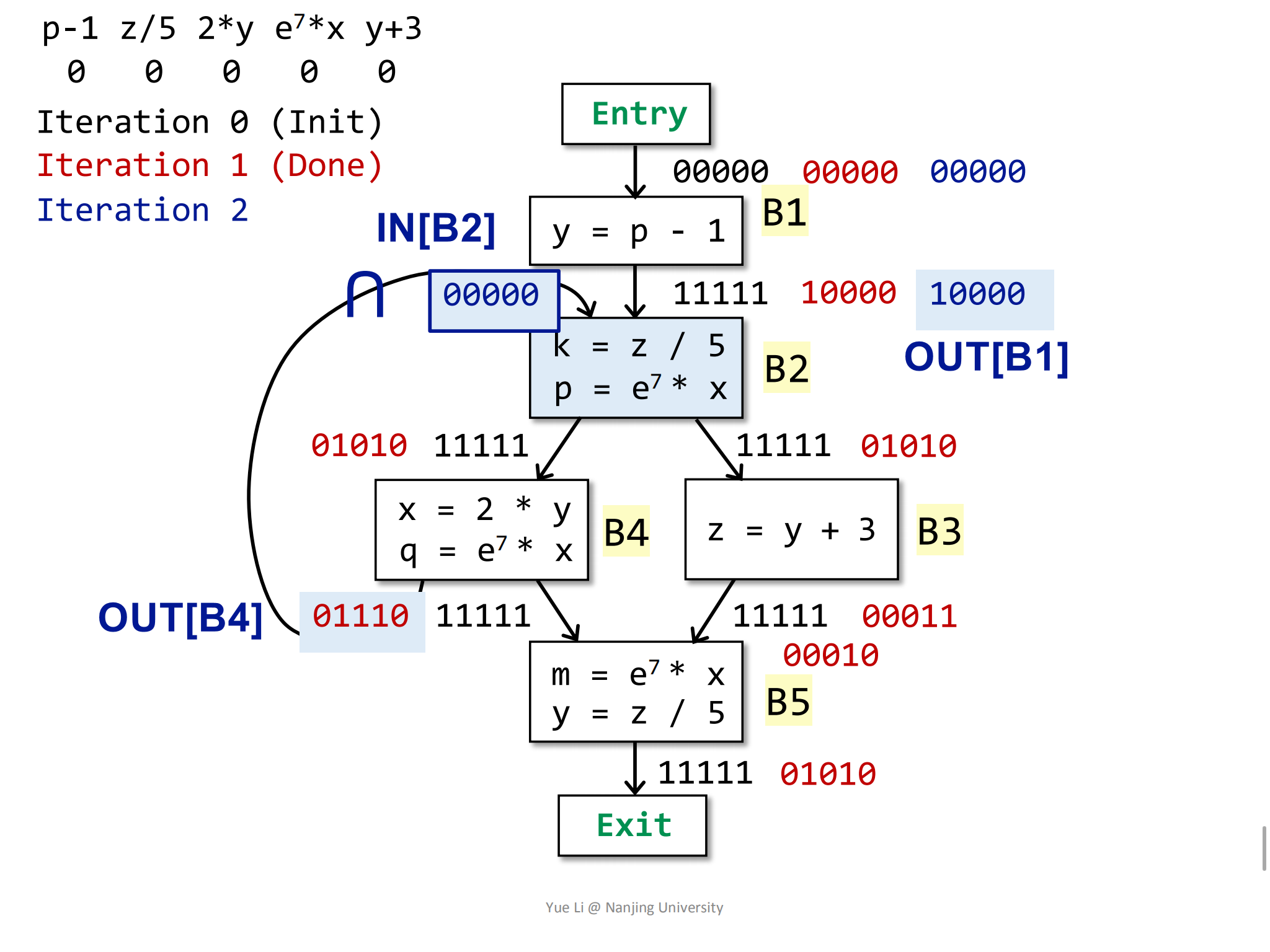
然后计算OUT:
1
2
3
4
5
6
7
8gen[B2] = { z / 5, e^7 * x } = 0 1010
IN[B2] = 0 0000
kill[B2] = { p -1 } = 1 0000
OUT[B2] = gen[B2] U (IN[B2] - kill[B2])
= 0 1010 U (0 0000 - 1 0000)
= 0 1010 U 0 0000
= 0 1010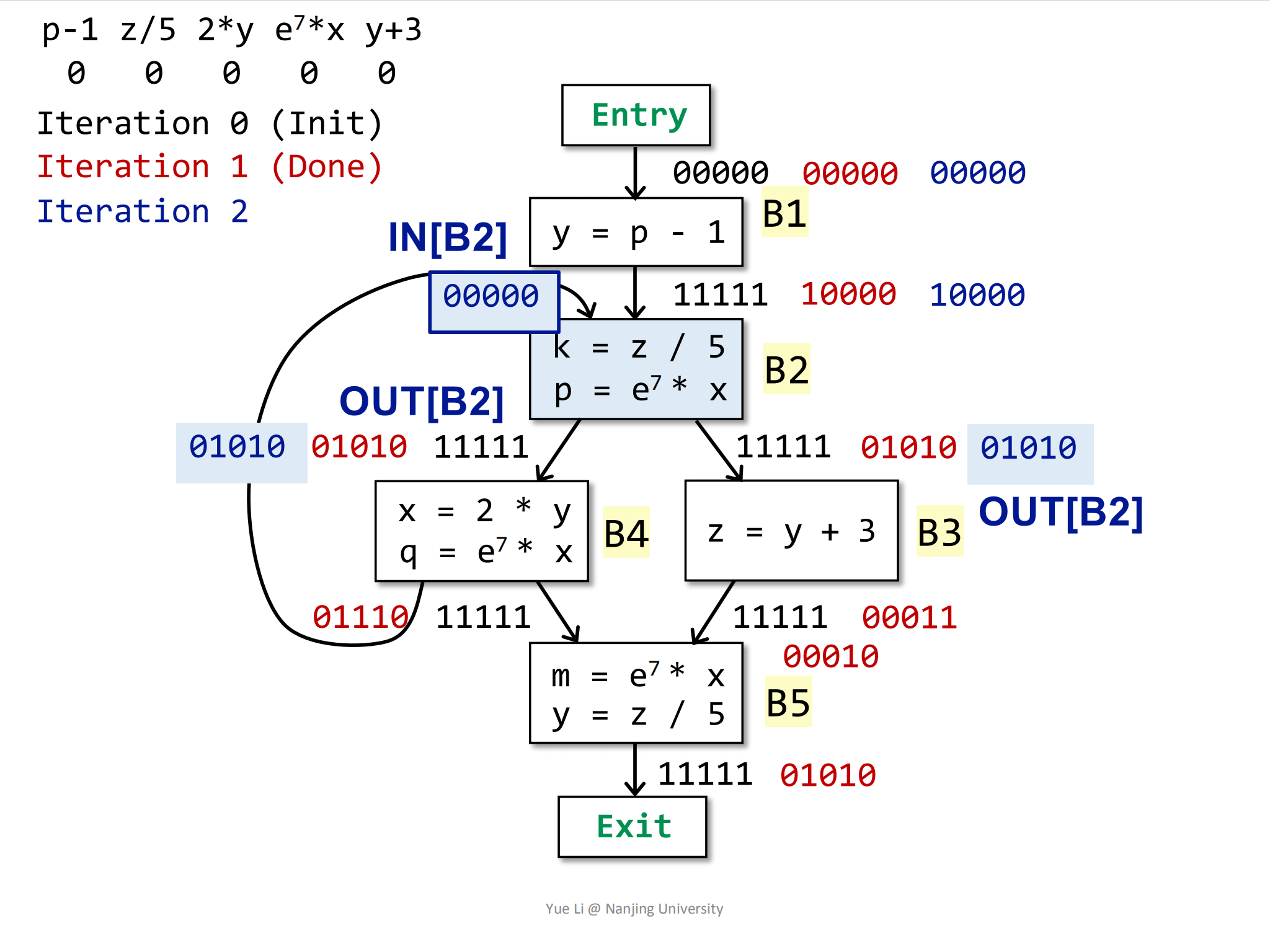
相比第一次迭代结果,
OUT[B2]也没有发生变化。然后计算B3块的
IN,其前驱块为B2,因为OUT[B2]没有发生变化,所以IN[B2]不变:1
2IN[B3] = OUT[B2]
= 0 1010同样的,
OUT[B2]也不会发生什么变化:1
2
3
4
5
6
7
8gen[B2] = { y + 3 } = 0 0001
IN[B3] = 0 1010
kill[B2] = { z / 5 } = 0 1000
OUT[B2] = gen[B2] U (IN[B3] - kill[B2])
= 0 0001 U (0 1010 - 0 1000)
= 0 0001 U 0 0010
= 0 0011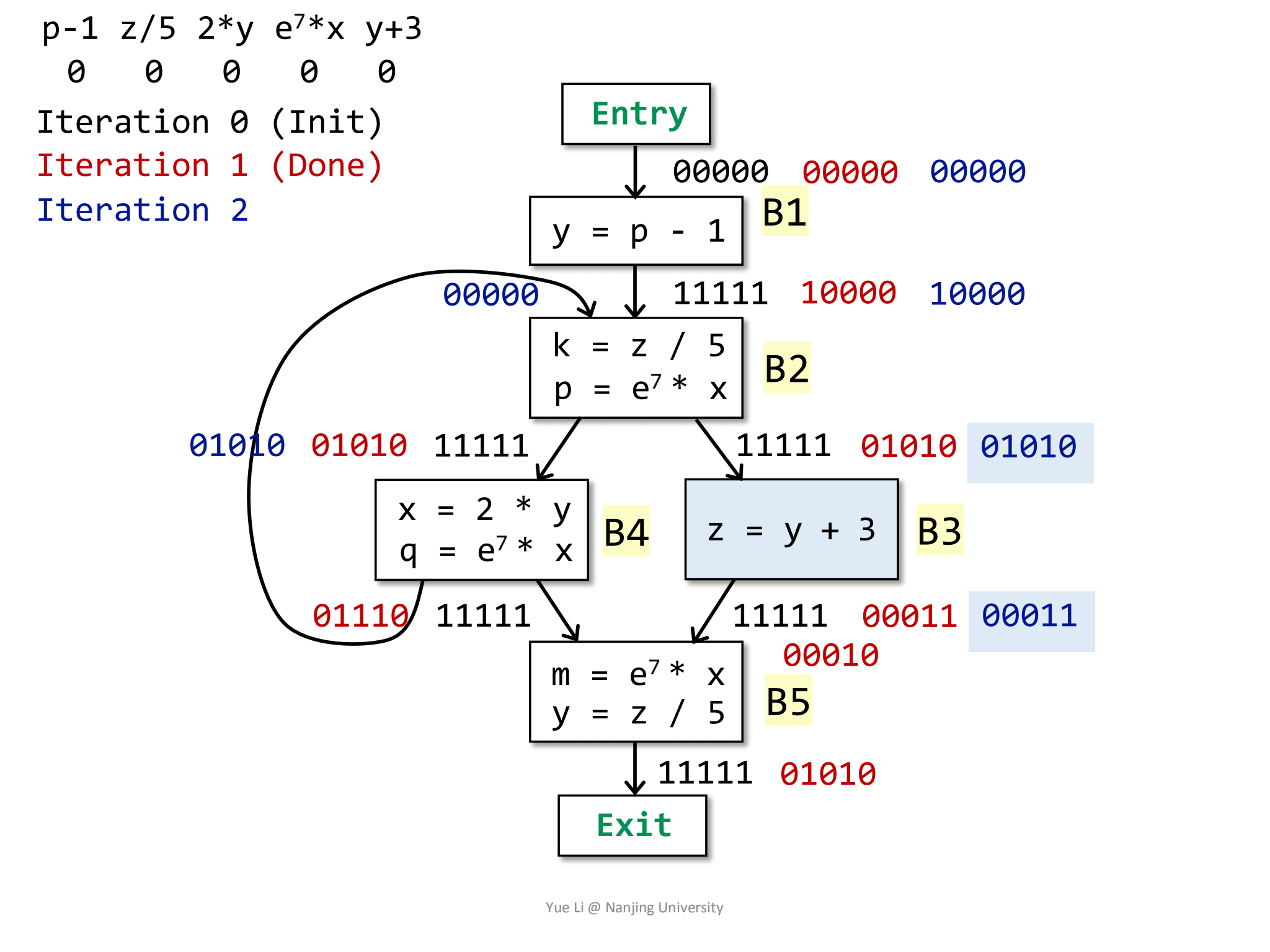
B4块的前驱也是B2,所以它和B3的道理一样:
1
2IN[B4] = OUT[B2]
= 0 1010OUT[B4]也不会发生变化:1
2
3
4
5
6
7
8gen[B4] = { 2 * y, e^7 * x } = 0 0110
IN[B4] = 0 1010
kill[B4] = { e^7 * x } = 0 0010
OUT[B4] = gen[B4] U (IN[B4] - kill[B4])
= 0 0110 U (0 1010 - 0 0010)
= 0 0110 U 0 1000
= 0 1110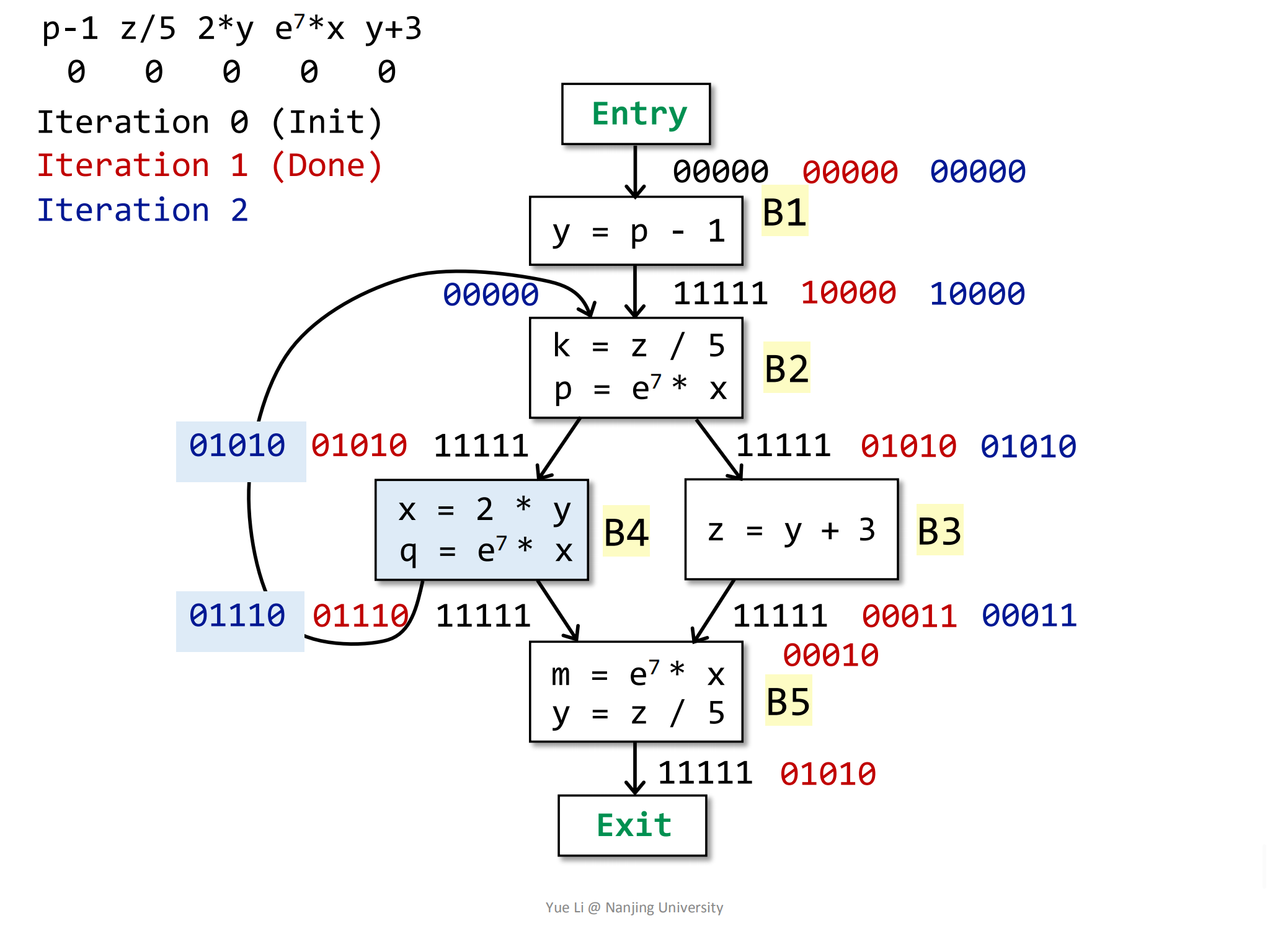
最后是B5,前驱块是
B3和B4,因为OUT[B3]和OUT[B4]都没有发生变化,所以IN[B5]也不会发生变化:1
2
3IN[B5] = OUT[B3] ∩ OUT[B4]
= 0 1110 ∩ 0 0011
= 0 0010IN[B5] = OUT[B3]IN[B5]没变,OUT[B5]也不会变:1
2
3
4
5
6
7
8gen[B5] = { e^7 * x, z / 5 } = 0 1010
IN[B5] = 0 0010
kill[B5] = 0 0101
OUT[B5] = gen[B5] U (IN[B5] - kill[B5])
= 0 1010 U (0 0010 - 0 0101)
= 0 1010 U 0 0010
= 0 1010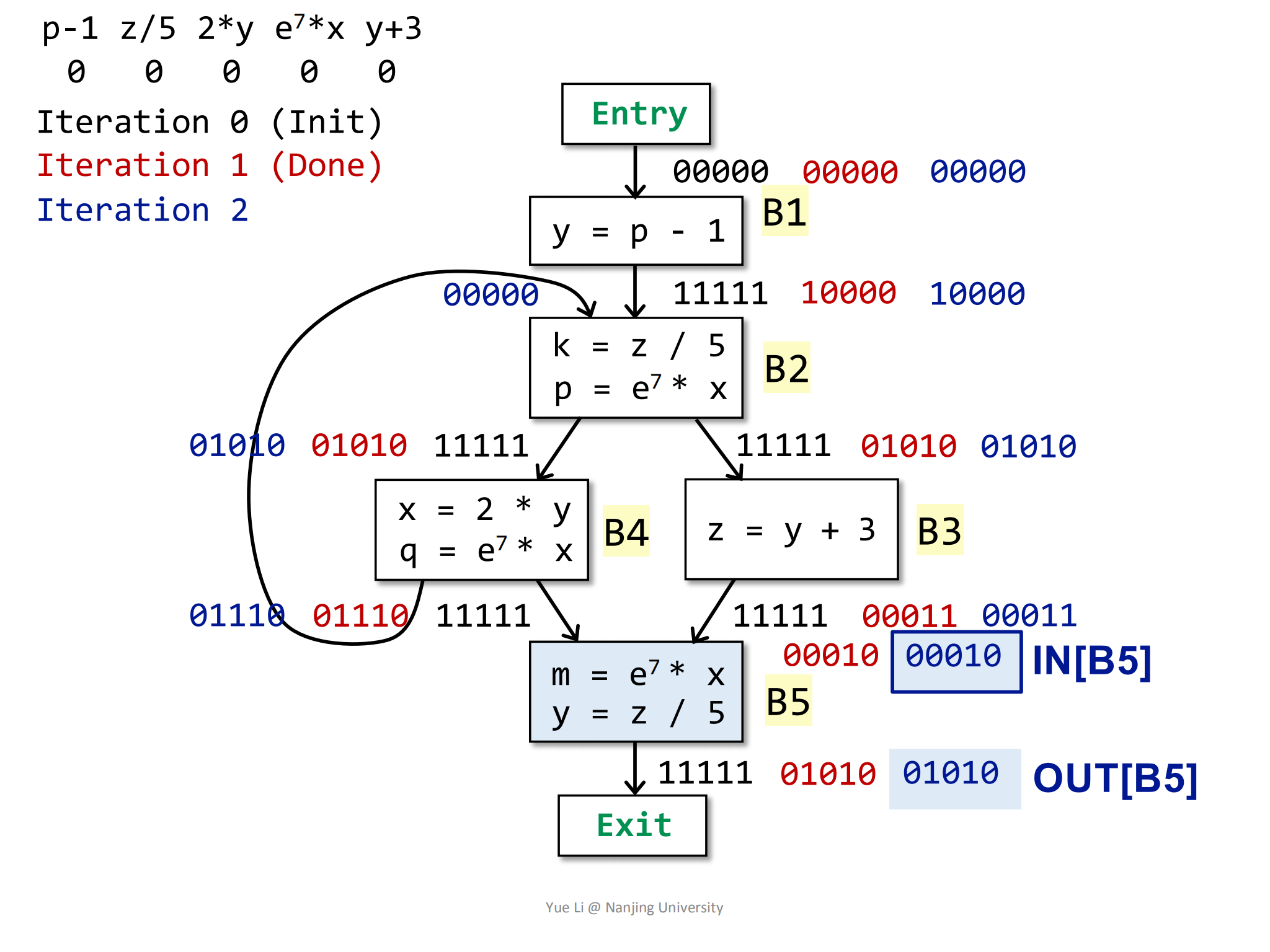
经过第二轮迭代,所有基础块的OUT都没有发生改变。算法到此结束。
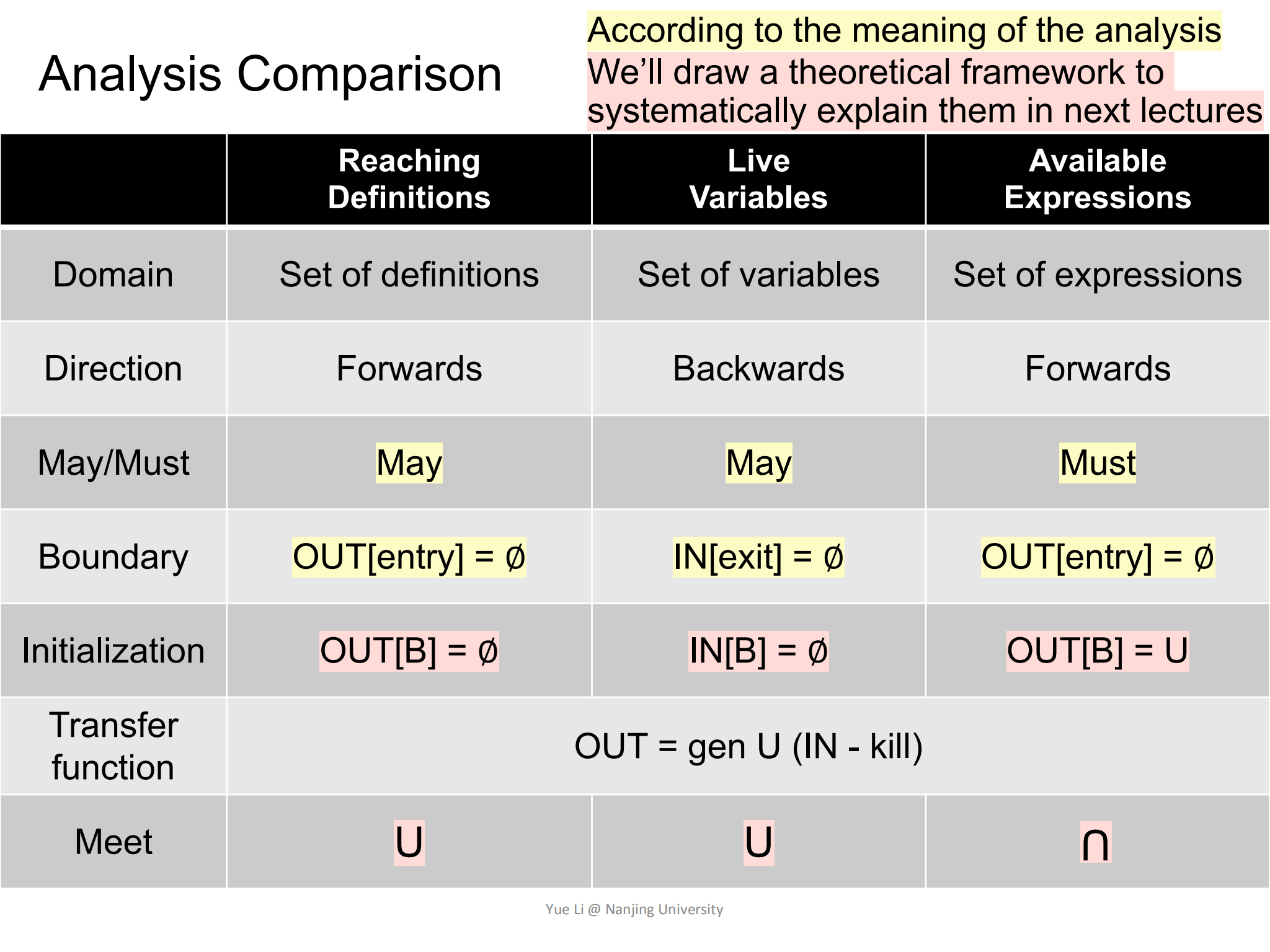
三种算法的比较
下图对Reaching Definitions Analysis,Live Variables Analysis 和 Available Expressions Analysis进行了简单的比较:
个人认为李樾老师讲的数据流分析很详尽,在讲解了原理的基础上,还会不厌其烦地用例子,带着我们一遍一遍地做迭代,自己遍历过一遍算法后,真的能理解地透彻很多,记忆也会深刻很多。